社内勉強会で因果分析力を身につけよう！

記事の挨拶

こんにちは、アナリティクスコンサルティングユニットの羅（ろ）です。今回は社内で取り組んでいる因果分析勉強会についてご紹介いたします。因果分析はマーケティング施策の効果検証や新薬の治験など、効果の有無を知るための統計的手法として広く用いられています。

はじめに

• 開催目的と動機

実務上で因果分析を効果的に活用するためには、必要なツールやコードを整備することが重要です。データ分析のための前処理や機械学習モデルの実装、因果関係の可視化ツールなど、適切なリソースを整えることで、案件において因果分析を使用するハードルを下げることができます。さらに、チーム内での共有やコードの説明資料を整えることも重要です。こうしたニーズに応えるには、データサイエンティストが理論と実装の両面でスキルを磨くことが必要です。
実は、社内のジュニアデータサイエンティストに「興味ある技術分野」のアンケートを取った結果、因果分析は常に上位にランクインしています。例年、新卒メンバーが主催した勉強会において、因果推論は人気でした。
さらに、近年、AIや機械学習の解釈性に対する関心が高まっており、関連する研究（深層学習など）とライブラリの利用が活発になっています。従来の案件（例えばマーケティングの施策効果検証、アンケート結果分析など）に加えて、予測の解釈性が重視される案件があります。例えば、金融、医薬品、法律などの業界は予測精度以外にも解釈性を重視する傾向があります。そうした場合に、迅速に対応できるようツールや資料を整備することが必要となります。
近年開発された深層学習モデルは高い予測精度を達成できる一方で、なぜその予測結果になったのかを説明することが難しいです。一方で、金融業界や医療業界といった分野では、単なる予測結果だけでなくその理由の説明も重要となっています。収集されたデータの背後にある因果関係を、擬似相関とバイアスを除去して明らかにする有力なアプローチの一つが因果分析です。当社では、近年注目されている因果推論の手法やツール・事例などに精通し、クライアントの要求に応じて適切なソリューションを提案できるよう常に心掛けています。そうすることで、予測解釈性が重視される分野の案件を獲得・遂行する上で大きなアドバンテージにもなると考えています。

• どうしたら習得できるか？ 独学v.s.勉強会

独学のメリットは、まず自己ペースで学習できることです。自分のスケジュールに合わせて学習時間を調整したり、自身の興味関心に合わせた内容を重点的に学ぶことができます。そして、Kaggleやオープンデータを使い、自身の興味や目標に基づいてプロジェクトや課題に取り組むことができます。実際のデータを使って因果関係を分析するなど、自分自身のアイデアや関心に基づく実践的な経験を積むことができます。
勉強会のメリットの目玉はチームでの学習とディスカッションです。 勉強会では他のメンバーと一緒に学習することで、相互の経験や知識を共有し、各ケーススタディのディスカッションを通じてより深い理解を得ることができます。加えて、参加メンバーの中には因果分析技術と案件経験豊富なメンバーが含まれるので、彼らのアドバイスやフィードバックを受けることで、より正確な因果分析の手法や考え方を学ぶことができます。また、勉強会のネットワーキングにより、同じ興味を持つ他のプロジェクトに参画した社員との交流機会があります。他のメンバーとの交流や協力を通じて、新たなアイデアやプロジェクトの可能性を見つけることができます。

• データサイエンティストの現場

当社のテクノロジーとビジネスを兼ね備えた人材を育てたいというミッションをふまえて、他の参加者に説明やプレゼンする機会を多く得られる勉強会を企画しました。勉強会では、因果分析の概念や手法を習得し、自分の言葉で理解を確かめ、相手が理解しやすい言葉を選んで説明できるようになることを目指しています。

勉強会の構成

1.目指すところ

a. 基礎知識:　因果推論の基本的な考え方（相関と因果の違い、擬似相関の種類、因果のグラフ表現）と手法（回帰分析、Meta-Learner法など）を学びます。
b. 実装:　Pythonを使用し、上記の代表的な手法を使ってデータに適用します。
c. トレンドウォッチ:　因果分析の研究は経済学分野で盛んであり、統計的な手法は古典的な手法とも呼ばれています。近年注目されている機械学習を用いた因果推論手法（反実仮想機械学習、深層学習による構造方程式の解法など）を把握し理解を深めます。
d. 勉強会のキックオフとして、参加者一人一人に期待値を設定していただきました（表1）。以下に代表的なものを共有します。

参加者	勉強会を通じて出来るようになりたいこと	因果分析が必要と感じること
参加者1	観測された事象から原因を特定するプロセスを体系的に学びたい＆それをデリバリーフローの1つの型としてまとめておきたい。	予測モデルや施策実施の結果を観察した時に、どんな情報が足りていないから誤差が生じているのか？なぜ仮説通りにならなかったのかをシステマチックに追跡できる手段を手に入れる必要があると感じる。
参加者2	分析はEDA(探索的データ解析)/モデル作りに加え、因果分析をやることで、分析の濃さを増やしたい。 今の案件上因果分析は可もなく不可もなく的な感じはする。が、出来ることによってメリットがある。	標準分析プロセス上にないこと（探索的データ解析->欠損埋め->訓練/テストデータセットの分割–>学習モデリング->チューニング）。
参加者3	各案件内で課題設定や分析設計を考える際に、因果推論による分析方法をアイデアの1つとして持っておきたい。分析方法の幅を持たせたい。	特にマーケティングでは本質的に因果の推論が必要と感じることがある（簡単な統計分析では関係性の主張を述べるのに十分に感じないことがある）。

2. 勉強会のコンテンツ

a. 記事共有:　因果分析に関する最新のニュースや事例紹介記事をメンバー間で共有し、その内容についてコメントします。参加者それぞれの興味は、ここで汲み取られます。
b. 輪読会:　因果分析に関する書籍を各章ごとで分けて、輪読会形式で内容をメンバーで共有しながら理解を深めていきます。

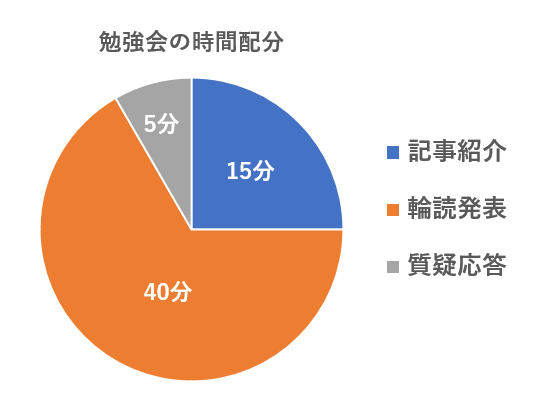
開催日程と参加人数

• 期間:　2022/11/17 ~ 2022/3/2 、約3か月半、計12回に亘って開催しました。
• 参加人数:　期初は12名でスタートし、期中から期末まで安定的に7名のメンバーが参加しました。
• 日程:　毎週木曜日の17~18時
• タイムテーブル:　15分の記事紹介、40分の輪読発表、5分の質疑応答。
• 輪読発表の準備時間:　書籍内容の理解に約2時間、発表資料の作成に約4時間かかりました。

3. 書籍の選定

書籍調査の結果、以下3本のベストセラーが候補としてリストアップされました。
1.『入門　統計的因果推論』J. Pearl ・M. Glymour・N.P. Jewell (共著), 落海 浩(訳) 2019 [文献1]
2.『効果検証入門〜正しい比較のための因果推論／計量経済学の基礎』安井 翔太 (著), 株式会社ホクソエム (監修) 2020 [文献2]
3.『つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門』小川雄太郎 (著) 2020 [文献3]

今回の勉強会の目的の一つは、因果分析の実装力を身につけたいため、小川氏の著作『つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門』を選びました。

その目次は以下の通りです。

　第1章 相関と因果の違いを理解しよう
　第2章 因果効果の種類を把握しよう
　第3章 グラフ表現とバックドア基準を理解しよう
　第4章 因果推定を実装しよう
　第5章 機械学習を用いた因果推論
　第6章 LiNGAMの実装
　第7章 ベイジアンネットワークの実装
　第8章 ディープラーニングを用いた因果探索

4. 記事紹介の内容

記事紹介で取り上げられた記事のうち、代表的なものを以下に挙げておきます（表2）。記事紹介を設けることで、書籍以外のコンテンツを勉強会内で議論することができます。

ラベル	タイトル	日付	リンク
病因学	急性散在性脳脊髄炎はコロナワクチンと因果関係がある可能性が高い	2022/11/10	https://agora-web.jp/archives/220915051454.html
因果推論	因果推論の道具箱	2022/11/10	https://www.jstage.jst.go.jp/article/ojjams/34/1/34_20/_pdf/-char/en
効果検証	MoT TechTalk #14 タクシーアプリ『GO』の施策検証、因果推論が解決します	2022/11/17	https://jtx.connpass.com/event/263378/?twclid=2-2vtxmc3wn952gwuf8ygbfu5eq
ツール	CALCというソニーが開発した因果分析ツール	2022/12/08	https://www.sonycsl.co.jp/tokyo/7593/
学会チュートリアル	Counterfactual Learning and Evaluation for Recommender Systems	2022/12/22	https://sites.google.com/cornell.edu/recsys2021tutorial

輪読発表の内容

輪読発表では、メンバー各自がメモ程度の資料を用意して臨みました。紙面の都合で全部は照会できませんが、第3章の資料の一部を紹介します（図2）。

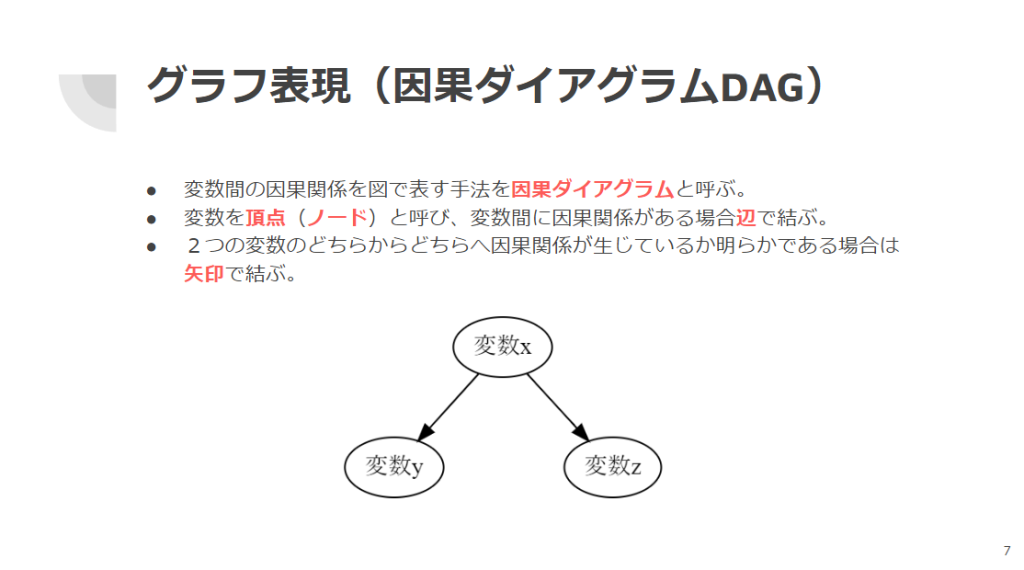
第3章のタイトルは「 グラフ表現とバックドア基準を理解しよう」です。この章ではまず構造方程式モデルについて紹介します（図3）。構造方程式モデルとは、変数間の因果関係を方程式で表現するモデルのことです。そして、方程式のグラフ表現として、変数間の因果関係を図で表す手法を因果ダイアグラムと呼びます（図4）。変数を頂点（ノード）と呼び、変数間に因果関係がある場合辺で結びます。２つの変数のどちらからどちらへ因果関係が生じているか明らかである場合は矢印で結びます。矢印で結んだ変数の関係を有向（Directed）と呼びます。交絡変数は、調査対象の変数と因果関係の両方に影響を与える要因です。

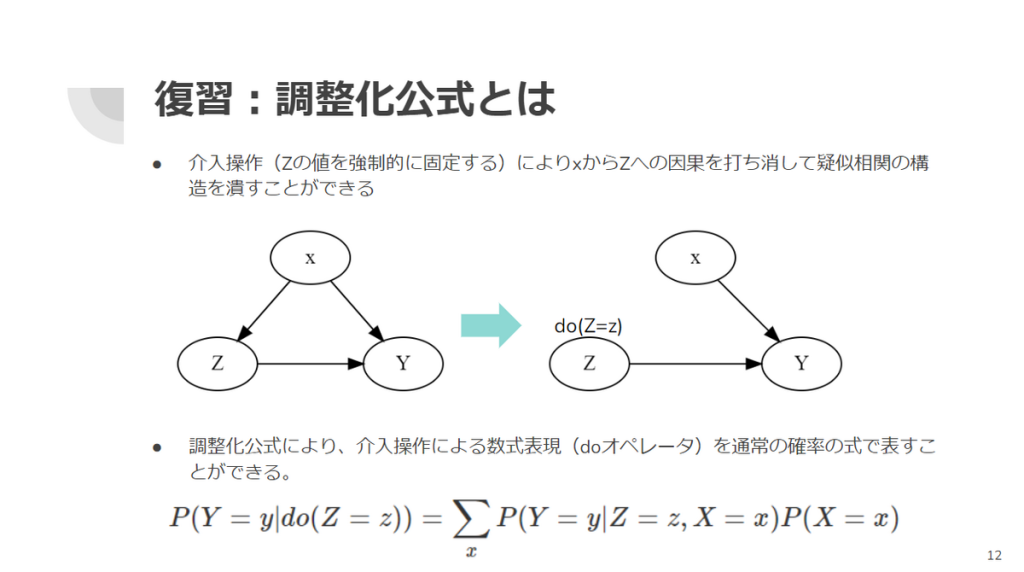
ところで、変数 Z から変数 Y への因果の大きさを推論する際に、Z から Y へ向かう矢印以外に、変数 X を介して Z と Y を繋ぐ経路が存在するダイアグラムのうち、X が交絡変数であるダイアグラムを特定するための基準があります。この基準（バックドア基準）によれば、X から Z と Y のそれぞれに向かう矢印で結ばれている場合、X は交絡変数であり擬似相関の原因となります（図5）。このような X については、Z について介入操作を行って X から Z への影響を除外する（X から Z への矢印を消す）ことにより、擬似相関の影響を除いた因果効果を推定することができます（図6）。

因果分析で押さえるべき5つのポイント

ここで、勉強会を通して学んだ因果分析で押さえるべき5つのポイントについて紹介します。

1.相関と因果の違いを理解する

「風が吹くと、桶屋が儲かる」ということわざがあります。もし毎日の風速データと桶屋の売上データがあるとしたら、二つのデータの相関が出るとは言い切れません。しかし、このことわざは、以下のストーリーにより相関があると主張します。風が吹くと、砂が舞い上がり、砂が目に入り、目が悪くなる人が増えます。その結果、三味線で生計を立てる人が増え、三味線が売れるようになります。三味線には猫の皮が使われるので、猫が捕られ、ネズミが増えます。ネズミは桶をかじるので、桶屋が儲かることになります。これは、一見すると相関のないところに因果関係があることを示す一例です（可能性が低い因果関係ではありますが）。

シンプソンのパラドックス

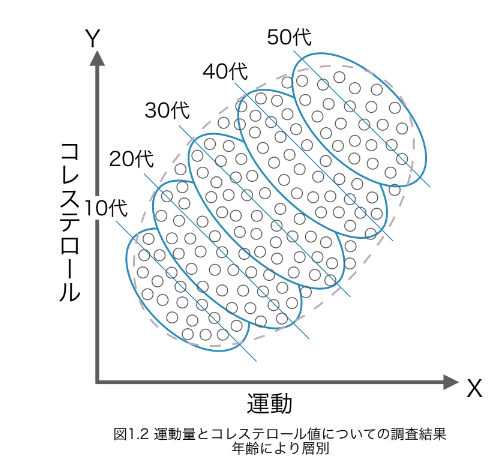
相関があるところに因果関係がない例はあるのでしょうか？ 例として、運動量と血液中のコレステロールのデータを見ていきましょう（図7）。まず、運動量が多い人はコレステロールの数値は少ないという医学的な事実がある前提でこのグラフを見ると、両者の傾向は右下がりのはずです。しかし、データは右上がりです。その理由は年齢という変数が入っているからです。各年齢層に分けてみると、前提の事実が成立しますが、全体でみるとそれと逆の結論が出てしまうという現象は、シンプソンのパラドックス（逆説）とも呼ばれています。シンプソンのパラドックスは擬似相関の一種でもあります。

データサイエンティストにとって、グループ（年齢層）ごとのデータに見られる相関関係が、データ全体でも成り立つだろうという直感的な推測に陥りやすいですが、これは必ずしも正しいとは言えません。

出典: 入門 統計的因果推論

2. 擬似相関の種類を把握する

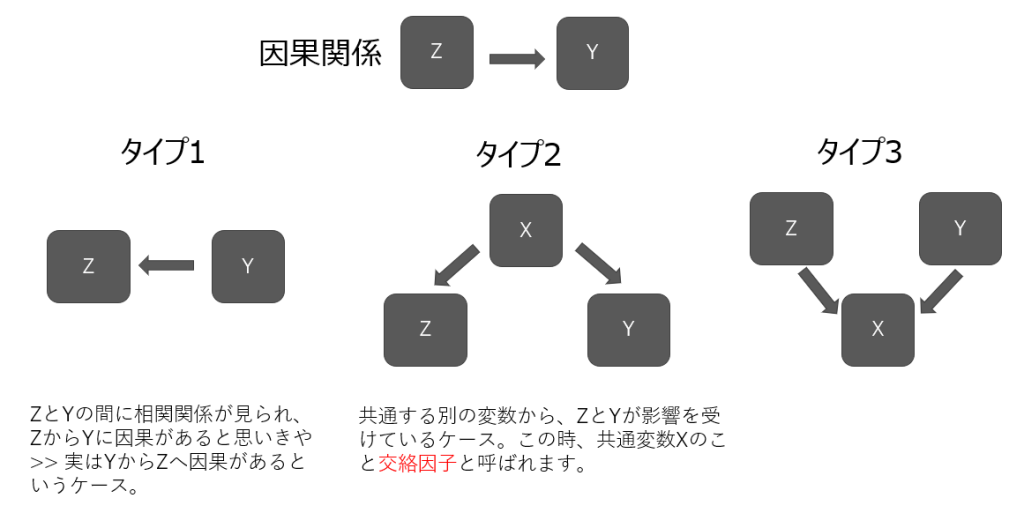
擬似相関とは、2つの変数間に見かけの相関関係が観察されるものの、実際には因果関係がなく相関が偶然や第三の要因に起因するものをいいます。擬似相関には以下のような種類があります（図8）。

タイプ1：逆の因果関係
因果の方向が正しく特定されていない場合に生じます。例えば、睡眠時間と健康度の相関の場合、睡眠時間が健康度に影響しているように思われますが、健康度が睡眠時間に影響している可能性もあります。

タイプ2：第三の変数に起因する相関
2つの変数の関係が、実際には共通の第三の変数の影響に起因している場合です。例えば、アイスクリームの消費量とプールでの溺死事故の強い相関は、実は共通の第三の変数である気温の影響に起因します。猛暑の期間になるとアイスクリームの消費量が上がる一方で、プールに行く人も増えて事故発生の件数も増えますが、アイスクリームの消費が事故発生の原因ではありません。気温の上昇が両者の共通の原因です。この共通の第三の変数は交絡因子（Cofounding Factor）とも呼ばれています。

タイプ3：合流点での選抜
例えば、入社試験において、項目Xと項目Yを合計した総合評価Zが基準値を超えると合格と判定されます。ここで、基準値を超えた集団（合格ライン以上）を抽出すると、XとYの逆相関が見えます。しかし、項目Xと項目Yの間には相関がないはずです。2つの変数（事象）の間に相関関係が見られたからといって、そこに因果関係があるとは限りません。

他にも、偶然により生じる相関があります。例えば、2つの時系列データを分析する場合に、両者に因果関係がないにもかかわらず、一方で他方を回帰すると当てはまりが良くなる場合などです（見せかけの回帰）。このように、さまざまな要因から擬似相関が生じる可能性があることに注意を払い、因果関係を推定する際にこれらの可能性を考慮する必要があります。実際に因果関係があるかを判断するためには、相関以外の情報も重要となります。

データサイエンティストにとって、擬似相関の事例にはデモグラフィック情報（性別、年齢など）が絡んでいるケースが多いです。言い換えると、デモグラフィック情報がないデータには、擬似相関が出るリスクがあると意識しても良いと思います。

3. 因果推論の三つの仮説

●Consistency
因果推論の処置（もしくは介入）効果を考える時に、処置を受けた人の効果は「その人が仮に処置を受けた時」(反実仮想)と同じです。例えば、「運動している人の体脂肪率は、その人が仮に運動しているときの体脂肪率と一致する」というようなことです。

●Positivity
因果推論の処置効果を考える時に、処置効果Yの値は1か0とします。因果推論を行うためには、Y=1とY=0のどちらのデータも観測されていて、その確率は0ではない正の値を取るという仮説です。言い換えれば、Y=1か0の両方のデータが観測されなければ、因果推論は行えないというです。例えば、男性には処置群も対処群も十分な人数いますが、女性には施策を実施しない場合、男性には因果推論を実施できますが、女性にはできません。

●Exchangeability
因果推論に必要な仮説の1つで、効果を比較する2つのグループが、研究対象の処置以外のすべての面で平均的に同質であることを意味します。ランダム化により、処置が個人にランダムに割り当てられることで達成されます。しかし、ランダム化が不可能な観察研究では、交絡変数を調整することでConditional Exchangeabilityが達成されます。

これらの3つの仮説は、因果関係を推論する際に重要な仮説です。これらの仮説が成り立たない場合、観察されたデータから因果関係を推論することはできません。

4. 効果指標と反実仮想

因果推論においては、処置効果を測る指標が不可欠です、効果指標としては、主に以下の3つの指標があります。

• ATE（平均処置効果）は、すべての対象者に対する処置の効果の平均値です。
• ATT（処置群に対する平均処置効果）は、処置を受けた対象者のグループ（処置群）の効果の平均値です。
• ATU（対照群における平均処置効果）は、処置を受けなかった対象者のグループ（対照群）に対する平均処置効果を表します。

これら指標の意味を具体的な例で考えてみましょう。たとえば、新しい薬の効果を評価する場合、新薬を投与することが処置（もしくは介入）に当たります。処置しない患者には、新薬の代わりに偽薬（プラセボ）が投与されます。新薬を投与したグループが処置群、偽薬を投与したグループが対照群となります。ATEは、処置群と対照群のすべての患者に対する薬の効果（例えば症状の改善幅など）の平均値です。ATTは、処置群の患者に対する薬の効果の平均値です。

ATE, ATT, ATUは、因果推論において重要な効果指標です。効果指標の定義を考えるうえで重要なことは、ある個人に対して、処置することと、処置しないことは同時には存在しえない（どちらかは現実に反する）ということです。それを踏まえてATTやATUなどの効果指標は定義されます。ATTは処置群において、処置を受けた場合と処置を受けなかった場合の効果の差の平均値として定義されています。ところが、処置群に含まれる人は全員が処置を受けているので、処置を受けていない場合は現実と反します。このように、現実と反する場合を想定することを反実仮想と呼びます。では、処置群において反実仮想である「処置を受けなかった場合」の効果をどう推定するかというと、傾向スコアによる重み付けを利用します。詳細については、参考文献 [1] [2] の解説を読んでください。

5. 因果推論と因果探索の違い

因果推論と因果探索は、因果関係に関する知識を得るためのアプローチですが、アプローチ方法や目的において異なります。因果推論は、効果を見るための施策（あるいは実験）を行った結果をもとに、ある変数（原因）が別の変数（結果）に与えるの影響の大きさを推定する手法です。例えば、薬物Aが病気Bの治癒に効果があるかどうかを調べる場合、因果推論を用いて薬物Aの服用が病気Bの治癒に与える影響の大きさを効果指標として推定することができます。

一方、因果探索は、データだけから変数間の因果関係を明らかにする手法です。その目的はデータから因果関係の候補を探索的に見出し、新しい因果仮説を生み出すことです。実務上、因果探索は案件の初期段階で行うこと多いです。

因果効果の大きさを推定するタスクを因果推論と呼びますが、その場合、因果構造が分かっているという前提があります。因果構造は有向非循環グラフ（Directed Acyclic Graph, DAG）という形で表現されています。図に描くと、変数はノードに対応し、変数間に因果関係がある場合に両変数を矢印で繋ぎます。データ分析のよくあるケースは、観察されたデータしかない状況（介入などの情報がない）で因果分析を行います。これは一般的なテーブルデータを考えてもらうと分かりやすいと思います。因果構造と因果効果の両方を推定するタスクは因果探索と呼ばれています。

古典的な手法として、LiNGAM（Linear Non-Gaussian Acyclic Model）があります。LiNGAMは線形非正規非循環モデルの略で、変数間の因果関係を推定する統計モデルです。このモデルは、変数間の関係を線形回帰式で表し、回帰の誤差分布が正規分布でないことを仮定しています。さらに、変数間に循環関係がないことも仮定しています。

もう1つの方法はベイジアンネットワーク （Bayesian Network）です。LiNGAMと違い、ベイジアンネットワークは条件付き確率表（Conditional Probability Table）を変数間の因果効果の大きさの推定に使います。ちなみに、因果グラフはここではネットワークとも呼ばれています。実際にベイジアンネットワーク を構築する際には、ネットワークの当てはまりの良さを測るステップやネットワーク構造を探索するステップなど重要なステップが含まれています。

近年の深層学習の発展により、深層学習で因果探索をする手法もあります。勉強会では、書籍にあるSAM（Structural Agnostic Model）という手法が紹介されました。SAMは画像生成で定評のある敵対的生成ネットワーク（Genera tive Adversarial Networks, GAN）を使ってテーブルデータから特徴量間の因果関係を推定する手法です。 観測データにノイズを混ぜて同じ形式のデータを生成するモデルと、生成されたデータを観測データと識別するモデルを敵対的に学習させることで、観測データの背後にある因果関係を推定します。特に、特徴量間の因果構造の行列をデータの生成過程から学習するというアイデアが評価されています。

まとめと今後の展望

今回の因果分析勉強会に通じて、因果推論と因果探索の概念の理解に加えて、自ら因果分析用の擬似データを生成して実験をできたことは印象的でした。今回の勉強会では書籍のサンプルコードを使用しましたが、そのほとんどはscikit-learn（Python用の機械学習ライブラリ）を使用していて、理解しやすいです。因果分析のオープンソースのリソースは、他の機械学習タスク（予測や分類など）と違い、Kaggleのように積極的に情報発信するコミュニティがないのが現状です。だからこそ社内で有識者を集めて輪を広めたいと思っています。

最近の大規模言語モデル（Large Language Model, LLM）の発展は、因果分析に新たな可能性を開いています。例えば、既存の因果探索の手法では、統計的に有意な因果関係を見つけることはできても、最終的な因果関係の特定は、分析者やその分野の専門家の判断に委ねられます。LLMの登場により、このステップを人工知能により代替することが可能になりそうです。LLMを活用しつつ、人間と人工知能が協調して作業を分担することで、因果関係の判断といった人間の専門知識を必要とするタスクも、LLMを介して誰でも容易に解決できることが期待されています。因果分析におけるLLM手法の活用例については、参考文献 [4] を参照してください。

参考文献

[1]『入門　統計的因果推論』Judea Pearl, Madelyn Glymour, Nicholas P. Jewell (共著), 落海 浩 (翻訳) 2019
[2]『効果検証入門〜正しい比較のための因果推論／計量経済学の基礎』安井 翔太 (著), 株式会社ホクソエム (監修) 2019
[3]『つくりながら学ぶ! Pythonによる因果分析: 因果推論・因果探索の実践入門』小川雄太郎 (著) 2020
[4] Causal Reasoning and Large Language Models: Opening a New Frontier for Causality

参考資料

本記事で紹介した手法のサンプルコードは、勉強会のテキストに採用した小川氏の著作 [3] の付録として github 上で公開されています。手法とサンプルコードの対応は以下の通りです。

• 擬似データの生成・可視化
  causal_book/1_3_pseudo_correlation.ipynb at master · YutaroOgawa/causal_book · GitHub

• LinGAM
  causal_book/6_3_lingam.ipynb at master · YutaroOgawa/causal_book · GitHub

• Bayesian Network
  causal_book/7_5_bayesian_network_pc_algorithm_20220421.ipynb at master · YutaroOgawa/causal_book · GitHub

• SAM
  causal_book/8_3_5_deeplearning_gan_sam.ipynb at master · YutaroOgawa/causal_book · GitHub