メルマガ登録

皆さん、こんにちは。マーケティングプラットフォーム本部で広告系製品の開発を担当している田頭です。
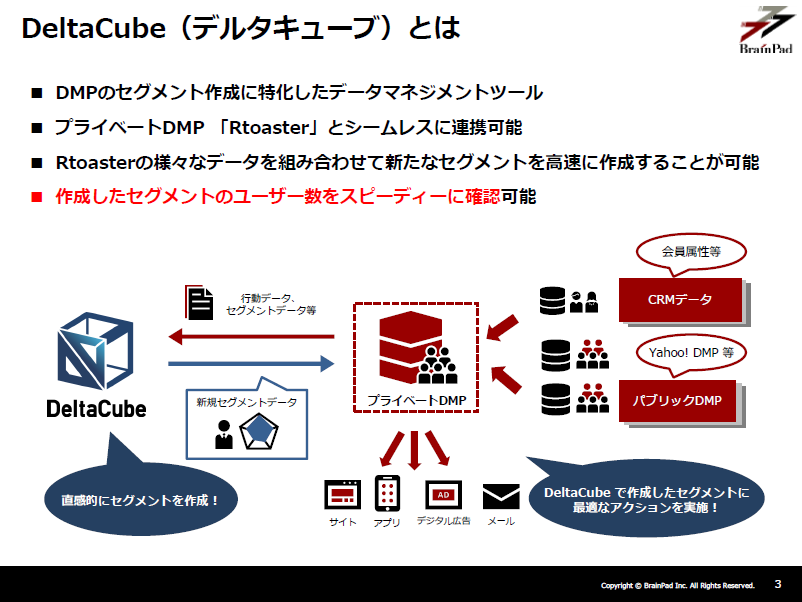
現在、ブレインパッドでは、DMP(※1)に蓄積されたさまざまなデータをもとに、ユーザー数を確認しながら直感的にセグメントを作成できる「DeltaCube(デルタキューブ)」という製品を提供しています。
ユーザーのセグメントを作成する際、担当者がストレスなくインタラクティブにセグメントの条件を設定しユーザー数を確認するためには、蓄積された大規模なデータの中から「高速に」ユニークユーザーの数を数えなければなりません。
このため、DeltaCubeでは、集計処理にPrestoと呼ばれる分散処理ミドルウェアを利用しています。
今回、このPrestoを利用したユニークユーザー集計の更なる高速化について検証作業を行いましたので、皆さんにご紹介したいと思います。
まずは「理論編」として、以下の内容を簡単に解説したいと思います。
内容についてさらに詳しく知りたい方は、ページ下部のスライドをあわせてご参照ください。
ストレスなく、インタラクティブにユーザー数を確認しながらセグメントを作成するためには、そのレスポンスの速度が非常に大切になります。
しかしながら、全ユーザーのトラッキングログなどの大規模なデータをもとにしているため、このユニークユーザー数の確認を厳密に行っていては、非常に遅いという問題があります。
そこで今回、セグメントのユニークユーザー数というのは「1人単位まで厳密にわかる必要はなく、全体に対するそのボリューム感がわかれば良い(つまり、推定値で良い)」という点に着目しました。

それでは、「ユニークユーザー数を高速に推定する」という今回のテーマについて、解説していきます。
DeltaCubeでは、Prestoという分散処理ミドルウェアを利用して集計処理を行っています。

PrestoはSQLクエリエンジンですので、当然SQLクエリを投げられます。
例えば、以下の状況を考えます。
このとき、Prestoでユニークユーザー数を求めるためには、以下のようなクエリを実行します。
SELECT
COUNT(DISTINCT uid)
FROM
t_log_data
WHERE
(絞り込みたい条件)
;ただし、ここでは厳密に集計処理を行っているため、実行速度は低速となります。
しかし、PrestoにはCOUNT(DISTINCT x)の推定値を返す関数approx_distinctが用意されています!
Prestoに用意されている(概算)集計関数の一つで、前述の通り「COUNT(DISTINCT x)」の推定値を返す関数です。
使い方は簡単で、前述のユニークユーザー数を求めるためのクエリであれば、以下のように記述することでその推定値を求めることができます。
SELECT
approx_distinct(uid)
FROM
t_log_data
WHERE
(絞り込みたい条件)
;Presto公式ドキュメントのapprox_distinctの説明部分には、
This function should produce a standard error of 2.3%, which is the standard deviation of the (approximately normal) error distribution over all possible sets.
(標準誤差((おそらく正規)誤差分布の標準偏差)2.3%で値を返す)
とありますが、同時にこれは(推定であるため)、
It does not guarantee an upper bound on the error for any specific input set.
(ただし、これは全ての入力に対して誤差の上限を与えるものではない)
とも書かれています。
そこで、Presto内部のapprox_distinctの実装を追ってみると、HyperLogLogと呼ばれるアルゴリズムが利用されていることがわかりました。
以降では、まずHyperLogLogの理論的な面について調べた結果を、次にそのPrestoでの実装について、簡単に解説します。


HyperLogLogとは、上図の通り、(重複があってもよい)データのcardinalityを推定するアルゴリズムです。
では、HyperLogLogについて、簡単な例を挙げてその具体的な考え方を解説したいと思います。
user1
user2
user3
user1
user3
user4
user5ここでは、例として2個のレジスタM1, M2を用意し、その初期値を0としておきます。
レジスタとは、推定値計算のためにある値を保持しておくための箱だと思ってください。
レジスタごとに推定値は計算され、それらをもとに最終的な推定値を求めます。
※ここの手順は、通常はユーザーIDのリストの要素1つ1つに対して繰り返し実行されますが、説明の簡便のため、ハッシュ化やその後の処理を手順ごとでまとめています。
ユーザーIDのリストを1行ずつ読み込み、そのユーザーIDを2進数(例として32ビット)にハッシュ化すると、以下のようになったとします。
00100101011100010101010101110001
10111101011000000000000011010101
00011101011100111111111111000001
00100101011100010101010101110001
00011101011100111111111111000001
10001101011100010101010101110001
00101101000001010101010101010100ハッシュ値を、最初の\( b\)ビットとそれ以降に分割し、最初の\( b\)ビットで対応するレジスタを決定します。
ここでは、レジスタの数は2であるので、\( b=1\)とします(0の場合と1の場合の2通りで分けられる)。
先頭が0の場合はレジスタM1に、1の場合はレジスタM2に割り当てるとすると、それぞれの割り当て結果は以下のようになります。
0 0100101011100010101010101110001 -> レジスタM1に割り当て
1 0111101011000000000000011010101 -> レジスタM2に割り当て
0 0011101011100111111111111000001 -> レジスタM1に割り当て
0 0100101011100010101010101110001 -> レジスタM1に割り当て
0 0011101011100111111111111000001 -> レジスタM1に割り当て
1 0001101011100010101010101110001 -> レジスタM2に割り当て
0 0101101000001010101010101010100 -> レジスタM1に割り当て割り当てられたハッシュ値の先頭(ただし、最初の\( b \)ビットはレジスタの決定に用いたため除く)から、0が連続した個数\( p \)を数えます。
0 0100101011100010101010101110001 -> p = 1
0 0011101011100111111111111000001 -> p = 2
0 0100101011100010101010101110001 -> p = 1
0 0011101011100111111111111000001 -> p = 2
0 0101101000001010101010101010100 -> p = 1この中で、最も大きい\( p \)をレジスタM1の値として保持します。
ここでは、user3に対応するハッシュ値(0011101011100111111111111000001)の、\( p=2 \)が最も大きくなります。
よって、レジスタM1では、元データのcardinalityは\( 2^p = 2^2 = 4\)であると推定されます。
なぜ\( 2^p \)と推定されるのかについては、上図「HyperLogLogの基礎」もしくはスライドをご参照ください。
レジスタM1と同様に推定します。
1 0111101011000000000000011010101 -> p = 1
1 0001101011100010101010101110001 -> p = 3ここでは、\( p=3\)が最も大きいため、レジスタM2では、元データのcardinalityは\( 2^3 = 8\)であると推定されます。。
レジスタM1、M2で推定値が出ましたが、実はそれぞれは指数の推定値となっているため、単純な算術平均は望ましくありません。
そこで、率の平均が望まれているような場合に用いられる、harmonic mean(調和平均)を計算します。
(注)実際の論文中では、もっと複雑なnormalized bias corrected harmonic meanを計算しています。
「4」と「8」のharmonic meanは、以下のように計算されます(逆数の算術平均の逆数)。
$$ \frac{2}{\frac{1}{4} + \frac{1}{8}} = 5.333\cdots $$
そして、cardinalityは整数のため、ここでは四捨五入して、最終的な推定値は「5」であるとします。
必要なメモリについては各レジスタで\( p \)の数を保持するだけでよいので、
「レジスタの数 × \( p \)の保持に必要な最大のビット数」で済みます。
実はこれは驚くべき省メモリで、例えば32ビットのハッシュ値を利用して、レジスタの数を16にしたとすると、全体で必要なメモリはたった「16×5 = 80bit」です。
以上、HyperLogLogの基本的な考え方がお分かりいただけましたでしょうか?
実際にはもう少し複雑ですし、さらにその推定値の改善手法がいくつか提案されています。
例えば、今回の例ではcardinalityの推定値と真値が一致しましたが、実際にはデータのcardinalityの真値が小さいと誤差が大きくなってしまうであろうというのは、すぐに予想できると思います。
もう少し詳しく知りたい方は、スライドをご参照ください。
「3. approx_distinctとは」の段落の最後に、「Presto内部のapprox_distinctの実装を追ってみると、HyperLogLogと呼ばれるアルゴリズムが利用されていることがわかった」と書きました。
そこで、最後にHyperLogLogのPrestoにおける実装のどのあたりに記述があるのかを、少しだけご紹介したいと思います。
まずは、approx_distinctの実装を見てみます。
すると、ソースコードにそのまま「HyperLogLog」という文字列が出てきます。
さらに詳細を確認すると、内部では「Airlift」というパッケージを利用していることがわかります。
※Airlift:RESTサービスを構築するためのフレームワーク
では、利用しているAirliftにおけるHyperLogLogの実装を見ていきます。
https://github.com/airlift/airlift/blob/master/stats/docs/hll.md
ここでは、別のパッケージのHyperLogLogを利用するということはなく、そのまま実装されているようです。
Airliftにおける実装でわかったことを簡単にまとめておくと、以下3点です。
今回は「理論編」として、大量ログからユニークユーザー数を高速に推定するための背景やアルゴリズム(HyperLogLog)、そしてそのPrestoにおける実装と利用法について、簡単にご紹介しました。
特に、HyperLogLogのアルゴリズムの基礎的考え方は、単純でありながらとても賢く、とても面白いと思います。その改善提案にも、計算途中の結果をうまく利用するような賢いものがあります。ワクワクしますね!
また、Prestoは全てをインメモリでかつ分散して高速に処理しようという、一見すると力づくにも見えるコンセプトながらも、HyperLogLogのようなアルゴリズムも実装されており、非常に使いやすくなっています。
次回は、「実践編」としてパフォーマンス検証についての記事をアップしますので、よろしくお願いします!
(※1)DMP(Data Management Platform)とは、広告主・メディア・ECサイトなどが保有するさまざまな大量データを収集・分析し、主にマーケティング用途での利用・活用を可能にするデータ基盤のこと。
あなたにオススメの記事

2023.12.01
生成AI(ジェネレーティブAI)とは?ChatGPTとの違いや仕組み・種類・活用事例

2023.09.21
DX(デジタルトランスフォーメーション)とは?今さら聞けない意味・定義を分かりやすく解説【2024年最新】

2023.11.24
【現役社員が解説】データサイエンティストとは?仕事内容やAI・DX時代に必要なスキル

2023.09.08
DX事例26選:6つの業界別に紹介~有名企業はどんなDXをやっている?~【2024年最新版】

2023.08.23
LLM(大規模言語モデル)とは?生成AIとの違いや活用事例・課題

2024.03.22
生成AIの評価指標・ベンチマークとそれらに関連する問題点や限界を解説

