メルマガ登録

当社の社員が物理を専門としない人向けに量子アニーリングについて解説します!
こんにちは、A.I.開発部の太田です。
今回は量子アニーリングの簡単なシミュレータを作ってみたり、実際のD-Waveを使ってみた経験から、物理を専門としない人向けに量子アニーリングについて解説しようと思います。
(シミュレータのコードはgithubで公開しています。私自身、量子アニーリングについては最近勉強し始めたところなので、色々ご指摘いただけると幸いです。)
さて、私の所属する部署の役割として、機械学習・人工知能関連の技術調査や社内への展開を行っており、その一環として昨年12月に早稲田大学の田中先生をお呼びして開催した量子アニーリング勉強会が社内で大変好評でした。
昨年度は量子アニーリングに関する一般書籍が発売されたり、科学雑誌「Newton」でも特集されており、物理学者以外の一般の方にも、量子アニーリングが認知され始めているように感じます。また、今年の6月にはAQC2017(Adiabatic Quantum Computing Conference 2017)という量子アニーリング分野での最重要な国際会議1が日本で開催されることもあり、日本国内での盛り上がりは昨年以上になるのではないかと個人的には思っています。
「量子」という言葉を聞くと、何やら難しそうな印象を受けるかと思います。私も最近までは、「そもそもどうやって使うものなの?普通にプログラミングするの?何か物理的な操作をするの?物理の知識はどれくらい必要なの?」という状況でした。 そんな中、3月に運良く実際にD-Waveを操作できる機会2があり、その時に思ったのが
ということでした。
せっかくシミュレータを書いたし、D-Waveの使い方もわかったし、使うだけなら物理がいらないこともわかったし、コツコツ勉強してきたことを物理を専門としない人向けに展開するのも意味があるかな、と思ったので、可能な限り物理用語を使わずに量子アニーリングについて解説してみようと思います。
- 対象読者
- (物理学の専門的な知識のない)エンジニア・分析官
- 必要な知識
- プログラミングの基礎的な知識
- 行列演算ができる程度の数学の知識
- この記事でわかること
- 量子アニーリングマシンの使い方がなんとなくわかる
- 量子アニーリングマシンを使う上で必要となるイジングモデルへのマッピングの仕方がわかる
- 量子アニーリングのシミュレーション(量子モンテカルロ法)についてなんとなくわかる
- この記事でわからないこと
- 量子アニーリングの理論的側面
近年注目を浴びている「量子コンピュータ」の作り方には、大きく分けて2つあります。
1つ目は「量子回路方式(ゲート式)」と呼ばれるもので、1980年代から研究が続けられてきました。 もう1つが「量子アニーリング方式」と呼ばれるもので、1998年に東京工業大学の西森教授たちが提案した手法です。 現在一般的に使われているコンピュータ(本記事では古典コンピュータと呼びます)やゲート式の量子コンピュータが汎用的な問題を対象としている一方で、量子アニーリング方式は組み合わせ最適化問題に特化しており3、 その代わりに、扱える変数の数4はゲート式よりも圧倒的に多くなっています。
| 古典コンピュータ | ゲート式 | 量子アニーリング | |
|---|---|---|---|
| 動作温度 | 室温 | 極低温 | 極低温 |
| 扱える変数の数 | 非常に多い | 数個程度 | 〜2000個 |
| 対象とする問題 | 汎用 | 汎用 | 組み合わせ最適化問題 |
量子アニーリング方式は、できることが限られている反面、使い方はとてもシンプルです。
古典コンピュータやゲート式の量子コンピュータでは、自分のやりたいことを実現するには、まずプログラミングをしなければいけませんが、量子アニーリング方式の場合はパラメータを設定するだけです。一般のウェブサービスやウェブAPIを使うのと似た感覚です。
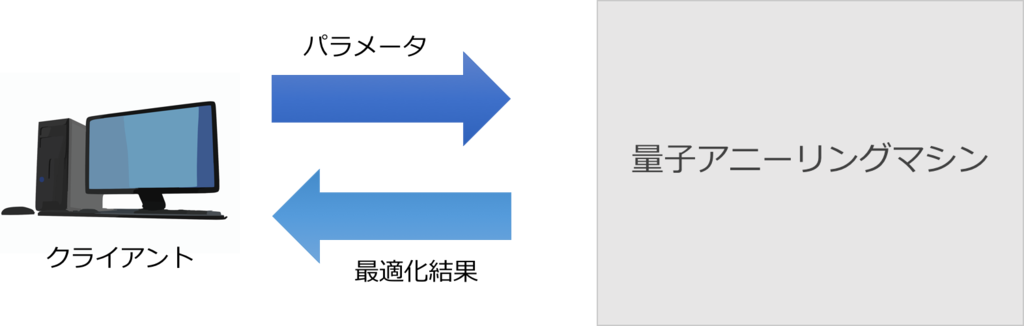
実際、世界唯一の商用量子アニーリングマシンであるD-Wave はインターネット経由でAPIをコールする形で利用可能です。D-Waveの実態を知るという意味で、以下の動画はとても面白いので興味のある方はぜひご覧ください。
量子アニーリングを利用するにはパラメータさえ設定できれば良いのですが、具体的にどんなパラメータがあるのかについて説明します。少し数式が出てきますが、ご容赦ください。
量子アニーリングは、組み合わせ最適化問題を解くことができるという点は先程述べたとおりですが、具体的には以下の関数を最小化する2値パラメータ\({s_i}\)の組み合わせをみつけることができます。
$$\begin{eqnarray} H &=& -\sum_{i \lt j}J^{ij}s_{i}s_{j} – \sum_{i}h^{i}s_{i} \\ s_{i} &\in& \{-1, 1\} \\ &&0 \le i \lt N \end{eqnarray}$$
ここで \({J^{ij}}\) および \({h^{i}} \)は実数値のパラメータです。
このように、最小化したい関数が \({s_{i} = \pm 1} \)の2次までで記述できる問題のことをイジングモデルといい、 \({s_{i}} \)のことをスピンと呼びます。スピンのかわりに \({x_{i} \in \{0, 1\}}\)を使って
$$ \begin{eqnarray} H &=& -\sum_{i \lt j}\tilde{J}^{ij}x_{i}x_j – \sum_{i}\tilde{h}^{i}x_{i} – c \\ x_{i} &\in& \{0, 1\} \\ &&0 \le i \lt N \end{eqnarray} $$
と書いた場合は QUBO (Quadratic unconstrained binary optimization)と呼ぶことが多いのですが、
\(\begin{eqnarray} x_{i} = \frac{s_{i} + 1}{2} \end{eqnarray} \)とすればお互いに変換することができるので、QUBOとイジングモデルは等価です5。 \(c \) は単なる定数なので、あってもなくてもよいのですが、 \(H \) を解釈する上で便利なことがあるので残してあります。
ちなみに、上の式から \(J \neq \tilde{J} \)、 \(h \neq \tilde{h} \)は明らかなのですが、手で変形しているとついつい忘れがちなので気をつけてください。
さて、数式だけ見てもイメージがつかないと思うので、簡単な例を見てみましょう。
最も簡単な例として、\( {N=2, J^{01} = 1, h^{0}=0}\) の場合を考えてみます。 この場合、\( {H}\) を展開すると
\( {H =-J^{01}s_0s_1 = -s_0s_1}\)となり、全ての\( {x_{i}}\) の組み合わせを書き下すと以下の表の通りになります。
| \(s_0\) | \(s_1\) | \(H\) |
|---|---|---|
| -1 | -1 | -1 |
| -1 | 1 | 1 |
| 1 | -1 | 1 |
| 1 | 1 | -1 |
\(H\)を見てみると、 \(s_0=s_1=1\)もしくは\(s_0=s_1=-1\)のとき、最小値 \(-1\)をとることがわかります。 量子アニーリングでできるのは、パラメータ \(J^{ij}\)、\(h^{i}\)などを受け取って、この \(s_0=s_1=1\)(もしくは \(s_0=s_1=-1\))という \(s_i\) の組み合わせを見つけることだけです。
このケースの場合は \(N=2\)なので、全ての組み合わせを列挙しても\(2^{N} = 2^2 = 4\)個だけでしたが、例えば \(N=100\)のときの組み合わせの数は、\(2^{100} = 1267650600228229401496703205376\)と膨大な数となります。この膨大な組み合わせパターンの中から最適なもの(正確には、 \( H\)を最小とする組み合わせ)を選んでくれるのが量子アニーリングです。
上記の例だけだと、具体的な使い方やどんなことに使えそうかイメージがわかないと思うので、2つめの例として、画像の修復を紹介します。 ここでは2値画像を対象としますが、グレースケール画像やカラー画像にも適用可能です。
以下のような2値画像があったとします。もともとはきれいな「量子」という文字でしたが、様々な経緯でノイズが混じってしまったという設定です6。この画像からノイズを除去することを考えます。

量子アニーリングを使うには、この問題を \(H\)という関数を最小化する問題に帰着させなければいけません。
まずはを画像をスピンで表す方法を考えます。 いろいろな方法が考えられますが、今回の場合は画像の各画素が2値なので、素直に各画素をスピンの値に対応させてみましょう。画素が1であれば、対応するスピンが+1、0であれば-1です。
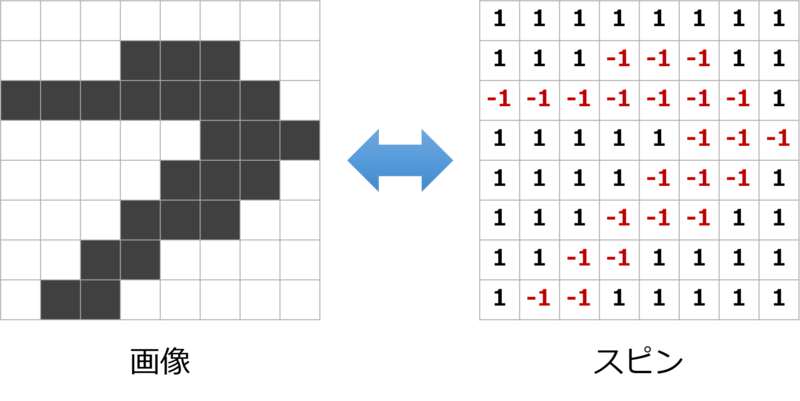
次に \(J \) や \(h \)を決めていきたいのですが、ノイズの混じっている画像以外に使えるデータがないので、いわゆる外部知識として、以下の性質を仮定します。
この2つの性質を満たすとき、 \(H \)が小さくなるような \(J \)と \(h \)を設定することができれば、量子アニーリングによって \(H \)を最小化し、その時のスピンを読み取ることで、上記の性質を満たすような画像を見つけることができます。
まず 1. については、 \(h^{i} \)をノイズを含む画像の \(i \)番目の画素の値(を \(\pm 1 \)になおしたもの)として、
$${ \begin{eqnarray} H_1 = – \sum_{i} h^{i}s_{i} \end{eqnarray} }$$
という項を入れれば良さそうです。
( \(i \) は2次元の座標 \( (x, y) \)に対応することに注意してください)
実際、すべての \(\pm 1 \)の組み合わせを見てみると、
| \( h^{i}\) | \( s_{i} \) | \( -h^{i}s_{i} \) |
|---|---|---|
| -1 | -1 | -1 |
| -1 | 1 | 1 |
| 1 | -1 | 1 |
| 1 | 1 | -1 |
と書き下せます。 この表から、例1のときのように\(h^{i} \)と \( s_{i}\) が等しい時に \( H_1\) が小さくなることが確認できます。
次に 2. についてです。こちらは、 \(J \)をスピンの足 \(i, j \)に依存しない正の定数として、
$${ \begin{eqnarray} H_2 = – J\sum_{\ll i,j \gg} s_{i}s_{j} \end{eqnarray} }$$
という項を考えます。ここで \(\sum_{\ll i,j\gg} \)は隣接する \( i\)と\( j\)についてだけ和を取ることを意味します。
\(J>0 \)であれば、 \(H_1 \)と同様にして \(s_i \)と \(s_j \)が等しい場合に \(H_2 \)も小さくなることが簡単にわかります。 両方の条件を満たすには、 \(H_1 \) と \(H_2 \)を単純に足したもの
$$\begin{eqnarray} H = H_1 + H_2 = – J\sum_{\ll i,j \gg}s_{i}s_{j} – \sum_{i}h^{i}s_{i} \end{eqnarray}$$
を小さくすれば、 \(H_1 \)も \(H_2 \)も小さくなりそうです。 \(J \)の大きさをどうしたらよいか、という問題はありますが、それは結果をみながら調整します。
簡単ですが、 \(J \)や \(h \)を設定するコードを示します。
WEIGHT = 1
NOISED_IMAGE = plt.imread('noised.png') # 0-1の np.ndarray
j = {}
for x in range(1, NOISED_IMAGE.shape[0] - 1):
for y in range(1, NOISED_IMAGE.shape[1] - 1):
# 隣り合う j のみ WEIGHT を設定
j[x, y, x, y + 1] = WEIGHT
j[x, y, x + 1, y] = WEIGHT
h = NOISED_IMAGE*2 - 1 # 0-1 を ±1 にこの \( j \) と \( h \) を量子アニーリングマシンに投げれば、ノイズの除去された結果がかえってきます。
とはいえ量子アニーリングマシンの実機は使えないので、シミュレーションをしてみました。 上記の \( j \) と \( h \) をシミュレータに投げてみた結果が以下となります。

元画像ではなくランダムなスピンで初期化しているので、ランダムだったスピンが徐々にそろっていく様子がわかるかと思います(上記のコードで定式化すると、左端と上端にゴミが残ります)。
このように、量子アニーリングを使うには、適切なパラメータを探し出す作業(イジングモデルへのマッピング)が必要となります。 マッピングの方法は問題毎に違うので、解きたい問題毎に \(H\) をどうするか考えなければいけません。 有名な問題についてはどうやったらよいかまとまっている論文 があるので、 より実践的な問題を解く場合は、この論文を参照しながら問題に合わせて \(H\)を構成していくのが良さそうです。
次に、もう少し複雑な例として、巡回セールスマン問題を紹介します。 巡回セールスマン問題は、「セールスマンが都市をまわるときに最小の移動距離で回りなさい」という問題です。この問題そのものをビジネスで応用する機会はあまりないかと思いますが、少し拡張することで配送計画の最適化など多彩な応用先があります。上述の論文にそって、下図のようにイジングモデルにマッピングします。
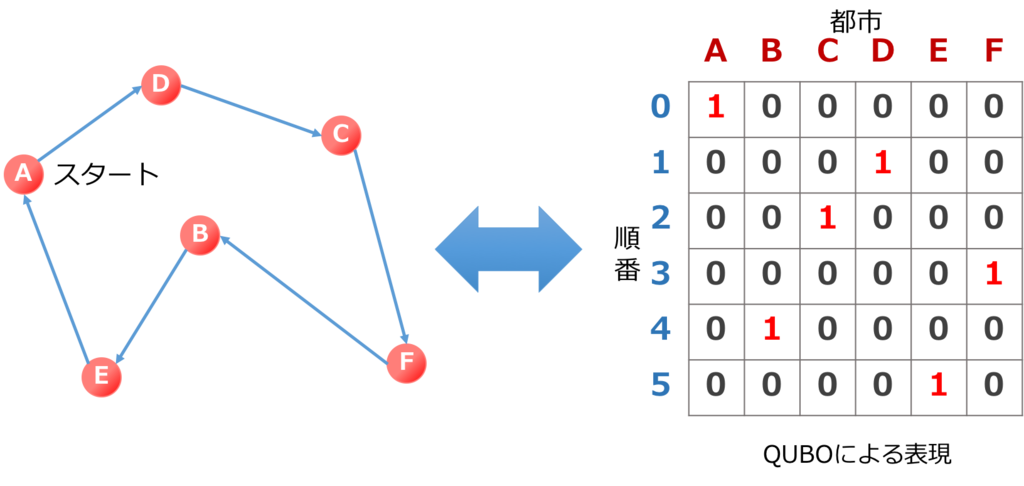
画像修復のときと違って、QUBO(変数が\({x\in\{0, 1\}}\))であることに注意してください。
Aに0番目(=スタート)にいるので、対応する\(x_{0,0}\)が\(+1\)でそれ以外が \(0\)、次にDに行くので、対応する\(x_{1,3}\)が\(+1\)でそれ以外が\(0\)、… というようになっています。 AとDの距離を\(d^{A,D}\)のように書くと、全都市を回ったときの総距離は
$${ \begin{eqnarray} H &=& \sum_{t,a,b}d^{a,b}x_{t,a}x_{t+1,b} \\ x_{t,a} &\in& \{0, 1\} \end{eqnarray} }$$
で表せます。ここで\(t\)は順番を、\(a\)、\(b\)は都市を表します。\(x\)について二次形式なので、量子アニーリングで最適化することができそうです。
実は上記の \(H\)の最小値は自明です。実際、全ての\(x\)が\(0\)のとき、\(H\) は最小値の\(0\)をとります。\(x\)が全て\(0\)の状態というのは「どこにも行っていない(移動距離は\(0\))」に対応しています。
当然これは求めたかった解ではありません。セールスマンには、全ての都市を回ってもらわなければいけません。 もう一度問題を見つめ直してみると、以下の条件が必要であることがわかります。
この2つの条件が満たされていれば、「セールスマンが全ての都市をまわること」を保証できます。 では、これらの制約をどうやってイジングモデルに取り込めばよいでしょうか?
シミュレーションするだけで良いのであれば、「そもそも制約を満たさない状態は探索しない」というアプローチ7がありますが、実際の量子アニーリングマシンを使いたい場合は、そういった制約を任意に追加することはできません。
そこで必要となるのが、\(H\)の修正です。 量子アニーリングマシンができるのは、あくまで \( H\)を最小にしてくれることだけです。 制約を満たしている場合にのみ、最小値をとるように \(H\)を修正することで、自動的に制約を満たしてくれるようにする必要があります。
それでは具体例をみてみましょう。まず1.の制約を変形してみます。
$$: { \begin{eqnarray} &\sum_{a}x_{t,a} &=& 1\\ \iff&\left(\sum_{a}x_{t,a} – 1\right)^2 &=& 0 \end{eqnarray} }]$$
この式は 全ての\(t\)で成り立たないといけないので、左辺をまとめて\(H_A\)と書くことにしましょう。
$${ \begin{eqnarray} H_{A} = \sum_{t}\left(\sum_{a}x_{t,a} – 1\right)^2 \end{eqnarray} }$$
この\(H_{A}\)が二乗の和の形になっているのがポイントで、どんな\(x\)に対しても必ず \(H_A \geq 0\)で、すべての\( t\)に対して制約を満たしている場合のみ、最小値の\(0\) をとります。
\(H\)のかわりに、以下の\(\tilde{H}\)を考えます。
$$ { \begin{eqnarray} \tilde{H} = H + A H_{A} \end{eqnarray} }$$
ここで\(A\)は非常にに大きな数とします。
\(A\)が大きいので、\(\tilde{H}\)を小さくするには、とにかく\(H_{A}\)を \(0\) にしなければいけません。 よって、\(\tilde{H}\)を最小とするのは\(H_{A} = 0\)のなかで\(H\)を最小にするもの、ということになります。\(H_{A} = 0\)が制約1. を表していましたから、この状態が「制約1.を満たしていて、かつ\(H\)が最小値をとる」状態になります。
制約2.についても同様の議論をすることができるので、結局\(H\)の代わりに
$${ \tilde H = \sum_{t,a,b}d^{a,b}x_{t,a}x_{t+1,b} + A \sum_{t}\left(\sum_{a}x_{t,a} – 1\right)^2 + A \sum_{a}\left(\sum_{t}x_{t,a} – 1\right)^2 }$$
を最小化すればよいことがわかります。 この式を展開して、\(J\) と \(h\)を求めるコードは以下のとおりです。 展開の際には、\(x \in \{0, 1\}\)なので、\(x_{t,a}^2 = x_{t,a}\)であることを使っています。
coeff = 2.0 # A の値を 距離の最大値 * coeff とする
n_cities = len(positions) # positions には都市の座標が入っている
j = collections.defaultdict(int)
max_dist = 0
# 第一項の部分を設定
for t in range(n_cities):
for a in range(n_cities):
for b in range(n_cities):
d = dist(positions[a], positions[b]) # dist は距離を計算する関数
max_dist = d if max_dist < d else max_dist
j[a, t, b, (t + 1)%n_cities] = -d
# Aは十分に大きくなければならない
A = max_dist * coeff
# 第二項の2次の部分を設定
for t in range(n_cities):
for a in range(n_cities):
for b in range(n_cities):
if a != b:
j[a, t, b, t] -= 2*A
# 第3項の2次の部分を設定
for a in range(n_cities):
for t1 in range(n_cities):
for t2 in range(n_cities):
if t1 != t2:
j[a, t1, a, t2] -= 2*A
# 1次の部分をまとめて設定
h = np.zeros((n_cities, n_cities))
for t in range(n_cities):
for a in range(n_cities):
h[a, t] += 2*A
# 定数部分
c = -2*A*n_citiesこの \( j\) と \( h\)、 \( c\) を量子アニーリングマシンに投げれば、最適解を得ることができます。(cはあってもなくてもよいのですが、あると \( H\) の値がそのまま距離になります) シミュレーションの結果はこちらをご覧ください。
上述の通り、量子アニーリングを使って最適化問題を解くには、以下のステップを踏みます。
先程の例では、3. の量子アニーリングマシンの部分をシミュレータで済ませましたが、 せっかくですので、ちょっと深掘りして、シミュレーションの仕組みについて紹介したいと思います。
量子アニーリングのシミュレーションに進む前に、そのもととなったシミュレーティッドアニーリングについて、簡単に説明します。
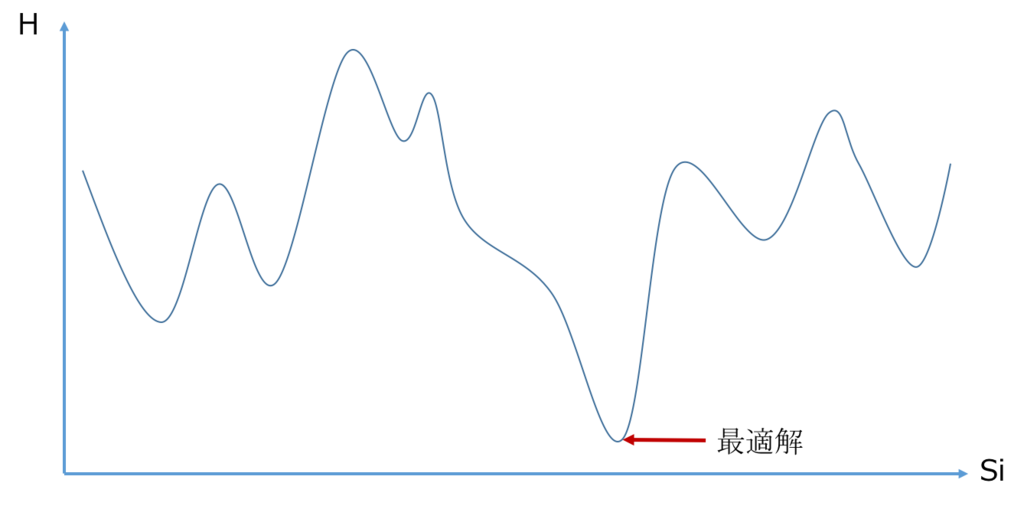
上図の縦軸は \( H\)、横軸は \( \{s_i\}\)(もしくは \( \{x_i\}\))を表していると思ってください。
(\( s_i\) は連続でないので、正確にはこのようななめらかな図にはなりませんが、イメージは伝わると思います。)
ここでやりたいのは、 \( H\) を最小にする \( \{s_i\}\) を見つけることです。
上述の通り、組み合わせの数は膨大で、全ての組み合わせを調べるわけにはいかないので、なるべく効率よく \( H\) の小さい点を探していきます。
最も簡単で、さまざまなアルゴリズムのベースとなるものとして挙げられるのは、近傍探索法と呼ばれる以下のような方法です。
- 適当に1点 \( s\) を決めて \( H\) の値を調べ、 \( E_1\) とする
- \( s\) の近くの点 \( \tilde{s}\) を適当に選び、 \( H\) の値を調べ、 \( E_2\) とする
- \( E_1\) と \( E_2\) を比較して、
- \( E_1\) のほうが小さかったら、なにもしない
- \( E_2\) のほうが小さかったら、\( \tilde{s}\) を新たに \( s\) とする
- 新たな \( s\) で上記を繰り返す
「下り坂をおりられるだけおりれば \( H\) は小さくなるよね」という発想です。 しかし、図のように凸凹がたくさんある場合は、山を超えることができずに局所的な最適解にトラップされてしまうため、そのような方法ではうまくいきません。
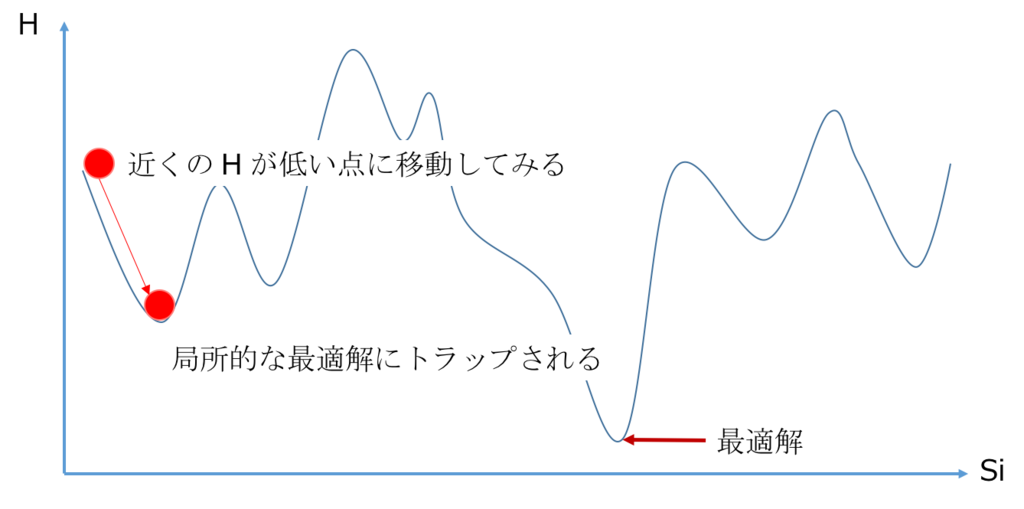
そこで、「適当な確率で山を飛び越えるようにしよう」というのがシミュレーティッドアニーリングです。
シミュレーティッドアニーリングでは、この山を飛び越える確率を、物理学でいうところの温度(の逆数)に対応するパラメータ \( \beta\) で調整します。具体的には、ある状態が実現される確率が
$$
{
\begin{eqnarray}
\exp\left(-\beta H\right)
\end{eqnarray}
}
$$
に比例するとして、\( \beta\) を小さい値から徐々に大きくしていきます。
(これは徐々に温度を下げていくことに対応します。)
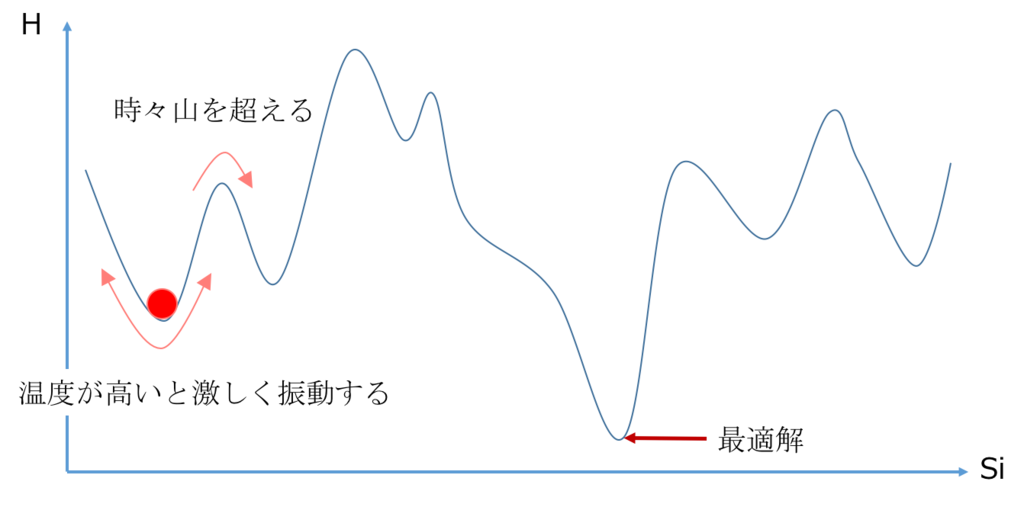
\( {\rm exp}\) の効果のおかげで、\( \beta\) が小さい時には大きな山を超えやすく、\( \beta\) が大きくなると、小さな山しか超えられないようになります。はじめは小さい \( \beta\) で山を飛び越えられるようにして色々な場所を探索してみて、最終的に \( \beta\) を大きくすることで、解を安定させます。
シミュレーティッドアニーリングのアルゴリズムは、以下のとおりです。
1. 適当に1点 s
を決めて H
の値を調べ、 E1
とする
2. s
の近くの点 s~
を適当に選び、 H
の値を調べ、 E2
とする
3. E1
と E2
を比較して、
- E1
のほうが小さかったら、確率 exp(−β(E2−E1))
で、s~
を新たに s
とする
- E2
のほうが小さかったら、s~
を新たに s
とする
4. β
を少し大きくする
5. 新たな s
で上記を繰り返すシミュレーティッドアニーリングは、温度を十分にゆっくりと下げていけば確実に最適解を得られることが理論的には知られていますが、温度の下げ方が速すぎると局所解にトラップされてしまう可能性があります。
シミュレータでは、確率的に s を選び直す部分と βを大きくする部分に分けて実装しています。 興味があればご確認ください。
シミュレーティッドアニーリングでは、1度に1つの点しか見ていないのに対して、量子アニーリングのシミュレーションでは、複数(ここでは \( m\) 個とします)の地点で同時に探索を始めます。
(この \( m\) のことをトロッタ数と言います。)

量子アニーリングで面白いのは、この \( m\) 個の状態が互いに独立ではなく、お互いに干渉しながら最適な状態を探していくことです。これによって、山の向こう側を「覗き見」しながら最適解を探せることになります8。
干渉が強ければお互いに同じ状態になろうとして、小さければお互いを気にせずに(局所的な)最適解を探すことになります。 同じ状態になろうとするとき、 シミュレーティッドアニーリングと同様に\( H\)が小さい方が実現されやすいようにしておくことで、徐々にエネルギーの低い状態に引き寄せられるように集まっていくようになります。
この干渉の強さを調整するパラメータを \( \Gamma\)(\( \Gamma\) が小さいほど干渉が強い)と書くことが多いのですが、この \( \Gamma\) は物理学では横磁場の強さと呼ばれているものです。\( s\) を磁石と見立てたときに、横から磁場をかけることに対応しています。
ちょっと話が抽象的なので、具体的な式で説明します。最適化したい関数 \( H\) を
$$
{
\begin{eqnarray}
H = -\sum_{i=1}^{n}\sum_{j=1}^{n}J^{ij}s_{i}s_{j} – \sum_{i=1}^{n}h^{i}s_{i}
\end{eqnarray}
}
$$
とします。量子モンテカルロ・シミュレーションでは、もともとの \( H\) の代わりに

を最小化します。
一気に複雑になった感がありますが… 第一項

は、括弧の中がまさに \( H\) と同じ形をしており、\( m\) 個のシミュレーションを同時に走らすことを表しています。
第二項の
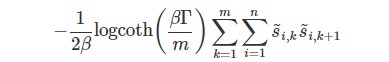
は、\( \tilde{s}_{i,k}\) と \( \tilde{s}_{i,k+1}\) との干渉を表しています。
\( \Gamma\) が小さくなると、 \( {\rm logcoth}(\frac{\beta\Gamma}{m})\) が大きくなり、干渉が強くなることがわかります。(干渉強ければ強いほど \( \tilde{s}_{i,k}\) と \( \tilde{s}_{i,k+1}\) は同じ値を取りやすくなります。)
シミュレータでは、\( \tilde{H}\) をここで定義していて、ここで \( \Gamma\) を更新しています。ご参考まで。
ここまでは、あたかもシミュレータのできることは量子アニーリングマシンの実機でもできるかのように書いてきましたが、実際にはいろいろな制約があります。
例えばD-Wave の最新版 D-Wave 2000Q であってもスピン数は高々2000個で、現実的な最適化問題を解くにはまだまだ足りません。また、スピン同士はキメラグラフと呼ばれる特殊な結合のしかたをしているため、\( J\) を任意に設定できたシミュレーションと違い、\( J\) の一部分しか設定することができません。このためイジングモデルへのマッピングがさらに難しくなっています。
こういった課題に対して、D-Wave の開発元である D-Wave Systems 社も無策ではありません。彼らは「2年ごとに量子ビット(スピン)の数を2倍にする」と公言して、実際にその公約を守り続けています。キメラグラフの話についても、彼ら自身がマッピング方法を解説していますし、大規模な問題を自動的に分割してD-Waveやシミュレーションで解いてくれるqbolvというソフトも公開していますので、今後は使いやすくなっていくものと思われます。
そもそも彼らは、「量子コンピューターなんて遠い未来の話」と言われていた時代から、冷ややかな視線も気にせず、自分たちの信念に基づいて研究を重ね、ついに商用の量子コンピュータを完成させた、アツい人たちですから、今後に期待せずにはいられません。
さて、D-Wave Systems 社が頑張っている一方で、実は日本勢もかなり頑張っています。
NEDO(国立研究開発法人新エネルギー・産業技術総合開発機構)「IoT推進のための横断技術開発プロジェクト」では、「組合せ最適化処理に向けた革新的アニーリングマシンの研究開発」というテーマが採択され、その中で量子アニーリングマシンの開発に取り組んでいます9。
量子アニーリングにこだわらず、イジングモデルを高速に解くという観点では、 例えば株式会社日立製作所は、従来のCMOS技術を使ったCMOSアニーリングという手法を開発し、産学連携で研究を進めていますし、株式会社富士通研究所はFPGAを使った技術を開発しています。内閣府主導のImPACTというプロジェクトでは、コヒーレントイジングマシンと呼ばれる方式の研究が進められており、その機能をクラウドで提供すると発表しています。
量子アニーリングを提唱した西森先生のお膝元である日本には、ぜひとも頑張ってもらいたいと思っています。
せっかくシミュレータを作ってみたので、その経験をもとに量子アニーリングについて解説しました。
当社では、データサイエンティストやエンジニアの方を積極的に採用しています。ブログに興味を持った方はぜひご応募ください! 他にもコンサルをはじめさまざまな職種で募集をしていますので、データ分析や当社の取り組みに興味のある方もぜひご応募ください。
https://www.brainpad.co.jp/recruit/
あなたにオススメの記事

2023.12.01
生成AI(ジェネレーティブAI)とは?ChatGPTとの違いや仕組み・種類・活用事例

2023.09.21
DX(デジタルトランスフォーメーション)とは?今さら聞けない意味・定義を分かりやすく解説【2024年最新】

2023.11.24
【現役社員が解説】データサイエンティストとは?仕事内容やAI・DX時代に必要なスキル

2023.09.08
DX事例26選:6つの業界別に紹介~有名企業はどんなDXをやっている?~【2024年最新版】

2023.08.23
LLM(大規模言語モデル)とは?生成AIとの違いや活用事例・課題

2024.03.22
生成AIの評価指標・ベンチマークとそれらに関連する問題点や限界を解説

