メルマガ登録

こんにちは、アナリティクスサービス本部の小田です。本連載ではレコメンデーションシステムについて、気の向くままにゆるゆると考察を行っています。第1回ではユーザベース協調フィルタリングの概念およびロジックについて考察を行いました。そして今回、ようやく訪れた連載第2回は、ユーザベース協調フィルタリングを実装し、実際のデータに対して適用してみたいと思います。
{recommenderlab}を利用した協調フィルタリングの適用協調フィルタリングをスクラッチで実装する前に、まず既存のパッケージを使って手っ取り早く試してみたいと思います。協調フィルタリングのようなポピュラーなアルゴリズムはパッケージとして出回っていますので、適用するだけならRでもPythonでも2-3行で可能です。
まずは利用するデータについての説明です。レコメンドシステム(recommender system)を研究・評価する際によく利用されるパブリックなデータセットがいくつかありますが、今回はその中でも最も広く利用されている「MovieLens」という映画の評価データを利用します。
その他のパブリックデータセットに興味がある方は、以下のウェブサイトにまとまっていますので、一読されると良いかと思います。アメリカンジョークのデータ(Jester)なども有名で、結構面白いです。ちなみにジョークのデータは評価スケールが100段階らしいです。日本にもお笑いの評価データとかあるんでしょうか。
MovieLensのトップページ(https://movielens.org/)
MovieLensデータセットは、パーソナライズされたレコメンドシステムの研究やベンチマークのために、ミネソタ大学のGroupLens Researchプロジェクトにより収集されているデータセットです。この研究のために運営されているMovieLens(https://movielens.org/) という映画作品レビューサイトの作品評価データで、MovieLensでは個人が自由に映画作品を評価・レビューできます。データセットは取得された時期やデータサイズ(ユーザ数や作品数)によっていくつか種類があるのですが、今回は1998年にデータ公開された小規模なデータセットを利用します。データ概要は次のとおりです。
MovieLensなどの有名なパブリックデータは、RやPythonのレコメンデーション用パッケージに同梱されていますので、パッケージをインストールして簡単に利用することができます。本ブログでも、Rのパッケージ{recommederlab}に含まれるMovieLensのデータを使いたいと思います。
{recommederlab}パッケージは、レコメンドシステムのアルゴリズム比較やテストを行うためのプラットフォームの提供を謳っており、パッケージを使って協調フィルタリングや行列分解などポピュラーなアルゴリズムを簡単に試すことができます。
それでは早速MovieLensデータセットを読み込んで内容を確認してみましょう。
library(recommenderlab)
# データセットのロード
data('MovieLense')
# クラスの確認
class(MovieLense)
#> 'realRatingMatrix'
# 分かりやすくするため、おなじみのmatrix型に変換
MovieLense.mtx <- as(MovieLense, 'matrix')
# 行数、列数の確認
dim(MovieLense.mtx)
#> 943 1664{recommenderlab}からロードしたデータセットは、realRatingMatrixというパッケージ独自のスパース行列で保持しています。ここでは読みやすさを優先し、一般的なmatrix型に変換した上で処理を行う方針をとっています。
# 先頭部分の内容確認
head(MovieLense.mtx[,1:10])各行がユーザ番号、各列が作品名を表示しており、それぞれの評価値が1-5で記載されています(評価行列)。以下のように先頭部分を確認しただけでも、相当数の未評価NAが存在することが確認できます。
評価行列の内容(先頭部分)
| Toy Story (1995) | GoldenEye (1995) | Four Rooms (1995) | Get Shorty (1995) | Copycat (1995) | Shanghai Triad (Yao a yao yao dao waipo qiao) (1995) | Twelve Monkeys (1995) | Babe (1995) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 4 | 3 | 3 | 5 | 4 | 1 |
| 2 | 4 | NA | NA | NA | NA | NA | NA | NA |
| 3 | NA | NA | NA | NA | NA | NA | NA | NA |
| 4 | NA | NA | NA | NA | NA | NA | NA | NA |
| 5 | 4 | 3 | NA | NA | NA | NA | NA | NA |
| 6 | 4 | NA | NA | NA | NA | NA | 2 | 4 |
次に評価行列の全体像を画像で確認してみましょう。
# 評価行列のイメージ描写
image(MovieLense)評価行列の全体をプロット
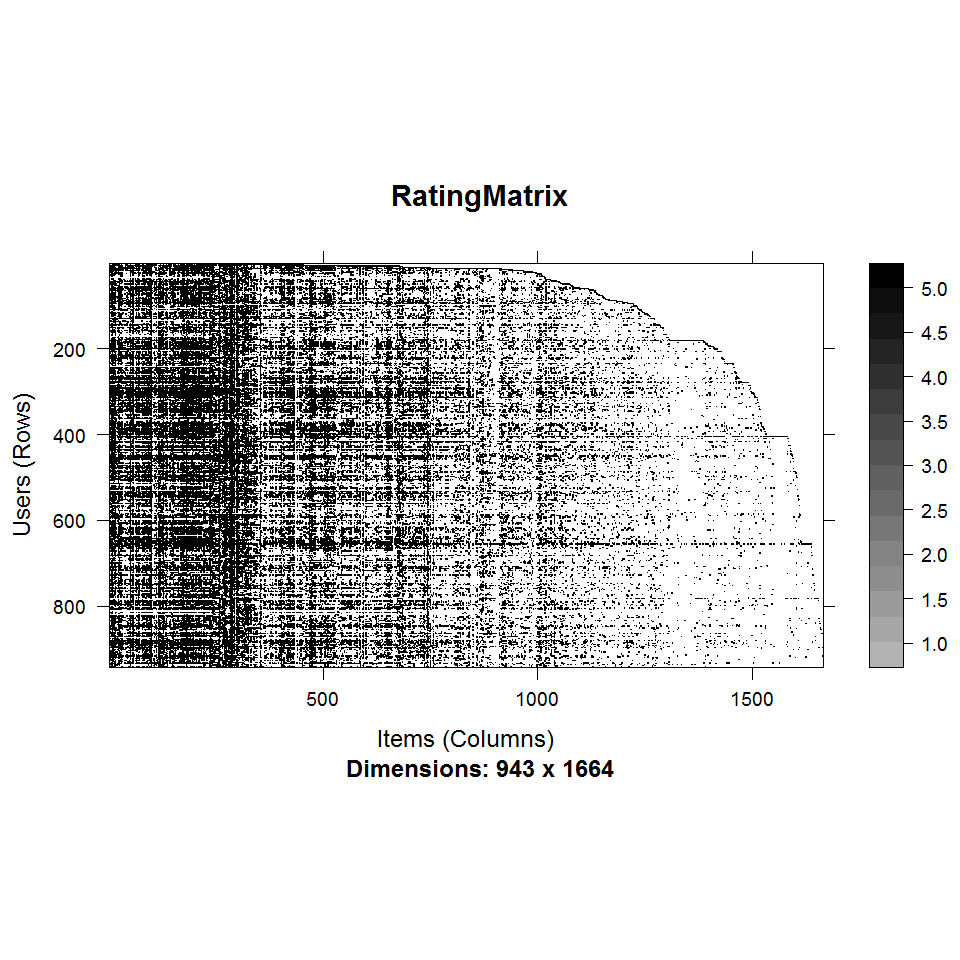
縦軸に各ユーザが、横軸に各作品が並んでいます。黒くなっている部分は評価5、白い部分は未評価NAです。なんとなく全体像を直感的に把握できたような気になります。
一人あたりの評価数の分布もついでに確認しておきましょう。
# 一人あたりの評価数の分布を確認
movies.per.user <- apply(!is.na(MovieLense.mtx), 1, sum)
hist(movies.per.user, main='number of rated movies')一人あたりの評価数の分布

全作品約1664に対して、ほとんどのユーザが数百程度の作品しか評価していないことがわかります。
{recommenderlab}で協調フィルタリング{recommederlab}のgithubページのREADMEに記載された例を参考に、ユーザベース協調フィルタリングを適用してみます。今回はユーザ番号1~100番のユーザの評価データを使ってユーザ番号101番のユーザに対してオススメの上位10作品をレコメンドする ケースを想定します。コードは次のようになります。
# 1番目~100番目のユーザのデータを学習データとして利用
train <- MovieLense[1:100]
# ユーザベース協調フィルタリングの学習(厳密には学習ではない)
rec <- Recommender(train, method = "UBCF")
# 推定した評価値の確認
pred.ratings <- predict(rec, MovieLense[101], type='ratings')
# 評価値の高いTOP10を抽出
pred.ratings.topN <- head(sort(as(pred.ratings, 'list')[['101']],
decreasing=TRUE), n=10)
# 表示
as.data.frame(pred.ratings.topN)推定された評価値の上位10作品
| pred.ratings.topN | |
|---|---|
| Shawshank Redemption, The (1994) | 3.488621 |
| Fargo (1996) | 3.450421 |
| Raiders of the Lost Ark (1981) | 3.449037 |
| Titanic (1997) | 3.353159 |
| Indiana Jones and the Last Crusade (1989) | 3.349170 |
| Back to the Future (1985) | 3.287979 |
| Contact (1997) | 3.286931 |
| Empire Strikes Back, The (1980) | 3.284206 |
| Braveheart (1995) | 3.224034 |
| Princess Bride, The (1987) | 3.209573 |
主要部分のコードは学習と適用(推定)で実質2行です。超お手軽ですね。なお、{recommenderlab}ではRecommender関数のmethod引数の値を変えることで他のアルゴリズムを簡単に試すことが可能です。
# `recommenderlab`がサポートするアルゴリズム(例)
# アイテムベース協調フィルタリング
Recommender(train, method="IBCF")
# SVD
Recommender(train, method="SVD")
# Funk SVD
Recommender(train, method="SVDF")
# アソシエーションルール
Recommender(train, method="AR")前述の{recommenderlab}のような協調フィルタリングは基礎的な内容さえ理解していれば、スクラッチからでも比較的簡単に実装可能です。ただし実装するにあたり第1回で考察した内容から一歩踏み込んで留意すべきポイントがあります。
NAにどう対処するか
今回はこれらのポイントを押さえつつ、協調フィルタリングをスクラッチで実装してみたいと思います。
想定ケースは先程の{recommenderlab}と同じとします。
ユーザ番号1~100番のユーザの評価データを使ってユーザ番号101番のユーザに対してオススメの上位10作品をレコメンドする ケースを想定します。
第1回のおさらいになりますが、ユーザベース協調フィルタリングの実施手順は次のとおりです。
第1回の例では類似度を測る指標として、ユークリッド距離の逆数を使いました。ユークリッド距離はシンプルで大変馴染みのある指標なのですが、MovieLensのような評価値データにユーザベース協調フィルタリングを適用する際は、コサイン類似度を使うことが多いです。シンプルでかつ、過去事例で精度が良いことが確認されているから、というのが主な理由でしょう。 コサイン類似度は、作品評価値ベクトル空間においてユーザを表すベクトル同士がなす角と解釈できます。-1~1の値をとり、2つのベクトルが同じ方向を向いている場合は1になります。
コサイン類似度のイメージ
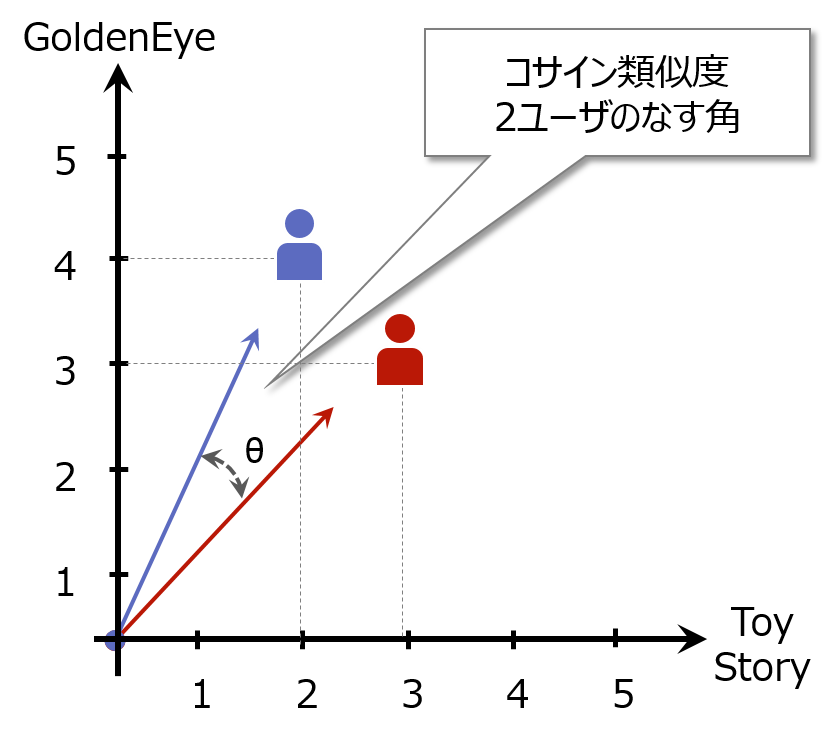
定義式としては次のようになっています。
コサイン類似度の定義式
$$ \displaystyle sim_{cosine}(a, b) = \frac{\sum_{y\in{items}}r_{ay}r_{by}}{\sqrt{\sum_{y\in{items}}r_{ay}}\sqrt{\sum_{y\in{items}}r_{by}}} $$
※\(r_{xy}\)をユーザ\(x\)のアイテム\(y\)への評価値とします。
コードで書くとこんな感じです。
# 2つのベクトルのcosine類似度を算出
simil.cosine.vec <- function(x, y) {
nume <- t(x) %*% y
deno <- sqrt(t(x) %*% x * t(y) %*% y)
return(nume / deno)
}実際には、レコメンド対象ユーザ(101番ユーザ)と各学習用ユーザ(1-100番ユーザ)同士の類似度を計算しますので、上記にアレンジを加えて、レコメンド対象ユーザの評価行列と各学習用ユーザの評価行列の2つを引数にとるような関数にします。一般的な類似度関数の仕様も、このように2つの行列を引数に渡せるようになっています。
# よくある類似度(距離)関数の形にする
# 第1引数と第2引数に行列をとる
simil.cosine <- function(X, Y=NULL) {
if (is.null(Y)) Y <- X
nume <- X %*% t(Y)
deno <- sqrt(diag(X %*% t(X)) %*%
t(diag(Y %*% t(Y))))
return(nume / deno)
}ユーザによって全体的に高い評価を付けがちな人(甘めの人)と、全体的に低い評価を付けがちな人(辛めな人)がいます。甘めの人がつけた評価4と、辛めの人がつけた評価2は、値は異なっていても実質的な意味合いには相違ないことがあります。類似度を計算する際にはこうしたユーザごとの評価の偏り(バイアス)をなるべく除外するために、事前に評価行列を中心化をすることが多いです。具体的には評価値から各ユーザの評価平均値を引いて、すべての評価値を「ユーザの平均値からの差」の表現に直してあげます。「この作品は、50番目のユーザにとって平均的な作品より1.5低く評価されている」のような表現です。この中心化された値でモデル構築、予測をした後、予測値に再度平均値を足してもとの評価値に戻します。
中心化のイメージ
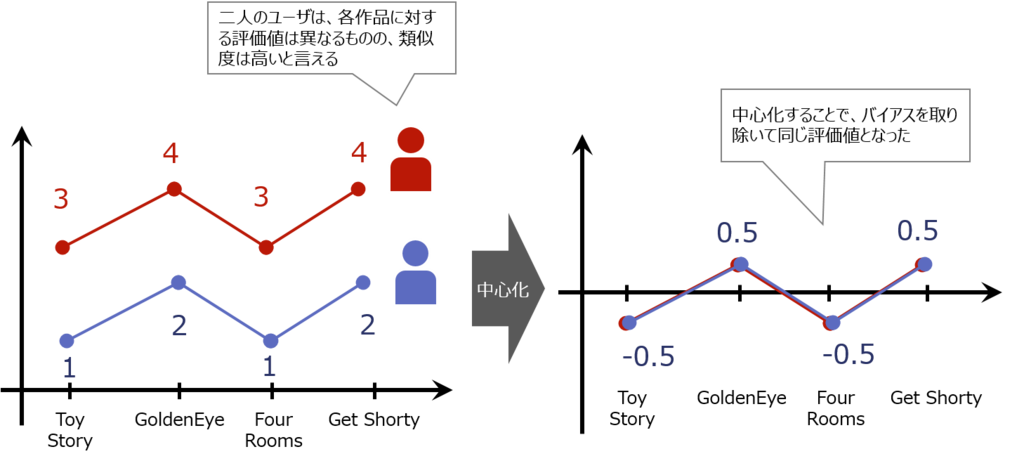
中心化のための関数は例えば次のようになります。
# 評価値を中心化する
centering.by.user <- function(X) {
center <- rowMeans(X, na.rm=TRUE)
X.norm <- X - center
return(list(data=X.norm, center=center))
}平均値も後で評価値を足し戻すときに必要なので、とりあえずlistに入れて返してます。
NAにどう対処するか上記で評価行列の内容を確認しましたが、評価行列は未評価NAという欠損だらけです。欠損をどう評価するかがひとつ問題となります。
欠損のある2ユーザの類似度は「2ユーザが共通して評価している作品のみで算出する(pairwise)」という方法がシンプルでわかりやすいのですが、2ユーザがともに評価している作品の評価値のみしか計算に使えないため、使えるデータが少なくなるという欠点はあります。この欠点への対処としては、平均値で補完するなどの、いわゆる欠損値の対処手法を適用することになります。{recommenderlab}の場合はどうしているかというと、未評価NAを0として解釈しています。内部的にna_as_zeroという変数があり、これがデフォルトではFALSEになっているので本来意図している挙動と異なりますが、最終的にコサイン類似度を計算している{proxy}パッケージの仕様に起因するようです。いずれにせよ結果として「ユーザが評価していない映画は、悪い評価を付けたのと同じだ」という解釈を前提としています。まあ、結構強めの条件ではありますが、類似度の計算としては欠損を考える必要もなくスムーズですね。。。最終的に精度が良ければ文句は出ないでしょう。
類似度を計算するとき、例えば共通して評価した5作品すべての評価値が一致する2ユーザと、共通して評価した20作品すべての評価値が一致する2ユーザではコサイン類似度は同じ1ですが、この2つのケースに違いはないのでしょうか。20作品すべてが一致した方が類似度の信頼性は高いと考えられます。この場合は共通する数が多いペアの評価値に重みをかけたり、一定数の共通評価をしていない類似度は無効にするなどの対処をすることはあります。
類似度の計算ができたので、最も類似度の高いk人のユーザを参考に、ユーザ101番の未評価作品の評価値を推定したいと思います。次のaとbのサブステップで実施します。
ユーザを類似度の降順で並べて、上位k件をとってくるだけです。
# 類似度の高い上位kユーザを取得
get.knn <- function(simil, k=25) {
knn <- head(colnames(simil)[order(simil, decreasing=TRUE)], n=k)
# 型の統一感のため、matrix型にcast
knn.mtx <- matrix(knn, ncol=length(knn),
dimnames=list(rownames(simil), 1:k))
return(knn.mtx)
}関数の途中でmatrix型にcastしていますが、この部分は整合性をとるために入れているだけなので重要ではありません。
類似度の高いユーザの意見(評価値)をより強く推定値に反映させるため、類似度の加重平均を算出し、前処理で中心化した分を足し戻した値が予測値となります。
評価の推定方法(加重平均)
$$\displaystyle r_{pred} = \bar{r}_{xy} + \frac{\sum_{x\in{\mathcal{N(a)}}} sim(a, x)\hat{r}_{xy}} {\sum_{x\in{\mathcal{N(a)}}}sim(a, x)} $$
※\( r_{xy}\)をユーザ\( x\) のアイテム\(y\)への評価値とし、\(\mathcal{N(a)}\)はユーザ\(a\)の最近傍ユーザ(k-nearest neighbor)の集合とします。
# 加重平均を算出する関数
mean.weighted <- function(target.id) {
target.nn <- nn[target.id,]
weighted.rating <- simil.mtx[target.id, target.nn, drop=TRUE] *
train.cen[target.nn, ]
mean.rating <- colSums(weighted.rating) /
sum(simil.mtx[target.id, target.nn])
return(mean.rating)
}
# 加重平均した評価値の算出し、平均値で足し戻す
weighted.mean.ratings <- mean.weighted(target.id)
pred.ratings <- target.cen.obj$center + weighted.mean.ratingsさて、”a. 類似度の高い上位kユーザを抽出”のkはどうやって決めたら良いのでしょうか。このkは近傍数と呼ばれ、上位何人の評価を参考にするかを調節する値です。一般にkが小さい場合は、類似度の高い少数のユーザの評価のみを参考にするため、一部の類似者の評価特徴が強く出た、嗜好の”尖った”予測になりやすいです。逆にkが大きい場合は、より多くのユーザの評価値の平均を予測に使うため、”なめらかな”予測になります。これは機械学習でいう「過学習」や「頑健性」の議論と同じで、kが小さい方が複雑で表現力は高くなりますが、一部の嗜好性のみに適合してしまいノイズに過剰に反応してしまう、いわゆる”過学習”が起きる可能性があります。一方でkを大きくしすぎると「頑健性」は高まるものの、細かい嗜好の差異をうまく表現できなくなる可能性があります。最適なkはケースバイケースではありますが、過去の研究から30-100の値を使うことが多いようです。{recommenderlab}ではデフォルト値が25人(k=25)となっていますので、今回のケースではk=25を使って推定をしています。
近傍数kによる違い

レコメンド対象のユーザがすでに評価している(視聴している)作品を除外した上で、推定した評価値が最も高い上位10の作品を抽出します。
# 未評価の作品に絞って評価値のTOPNリストを表示
pred.not.rated <- pred.ratings[is.na(target.mtx)]
head(sort(pred.not.rated, decreasing=TRUE), n=10)ここまでの内容を使ってレコメンド処理をすべて記載してみます。
# レコメンド対象ユーザの指定
target.id <- '101'
# 学習用ユーザとレコメンド対象ユーザの評価値を変数へ格納
train.mtx <- as(MovieLense[1:100], 'matrix')
target.mtx <- as(MovieLense[target.id], 'matrix')
# 評価値の中心化
train.cen.obj <- centering.by.user(train.mtx)
target.cen.obj <- centering.by.user(target.mtx)
# 中心化した評価の抽出
train.cen <- train.cen.obj$data
target.cen <- target.cen.obj$data
# NAを0で置換(議論の余地あり)
train.cen[is.na(train.cen)] <- .0
target.cen[is.na(target.cen)] <- .0
# レコメンド対象ユーザと学習用ユーザのコサイン類似度を計算
simil.mtx <- simil.cosine(target.cen, train.cen)
# 類似度の高い上位25人のユーザ番号を抽出
nn <- get.knn(simil.mtx, k=25)
# 加重平均した評価値の算出し、平均値で足し戻す
weighted.mean.ratings <- mean.weighted(target.id)
pred.ratings <- target.cen.obj$center + weighted.mean.ratings
# 未評価の作品に絞って評価値のTOPNリストを表示
pred.not.rated <- pred.ratings[is.na(target.mtx)]
head(sort(pred.not.rated, decreasing=TRUE), n=10)協調ベースフィルタリングは、スクラッチで書いても大した分量にはならないことが確認できると思います。上記の推定結果は、前述の{recommenderlab}での推定値と一致します。
上記のコードでは、わかりやすく見せるためレコメンド対象ユーザを101番一人だけに絞っていましたが、コードを一部変更することで複数ユーザのレコメンドリストも一気に算出可能です。以下リンクにコードの例を記載してます。
{recommenderlab}のモデルがやっていること{recommenderlab}での協調フィルタリングの実行例を冒頭で確認しましたが、中はどういう処理になっているのでしょう。実行部分のコードは以下の2行です。
rec <- Recommender(train, method="UBCF") # 学習
pre.top10 <- predict(rec, MovieLense[101], type='topNList', n=5) # 予測recオブジェクトの中身を確認してみましょう。
# recの中身を確認
str(rec@model$data)
Formal class 'realRatingMatrix' [package "recommenderlab"] with 2 slots
..@ data :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
.. .. ..@ i : int [1:10948] 0 1 4 5 9 12 14 15 16 17 ...
.. .. ..@ p : int [1:1665] 0 51 64 74 95 103 111 168 195 231 ...
.. .. ..@ Dim : int [1:2] 100 1664
.. .. ..@ Dimnames:List of 2
.. .. .. ..$ : chr [1:100] "1" "2" "3" "4" ...
.. .. .. ..$ : chr [1:1664] "Toy Story (1995)" "GoldenEye (1995)" "Four Rooms (1995)" "Get Shorty (1995)" ...
.. .. ..@ x : num [1:10948] 1.395 0.295 1.126 0.361 -0.207 ...
.. .. ..@ factors : list()
..@ normalize:List of 1
.. ..$ row:List of 2
.. .. ..$ method : chr "center"
.. .. ..$ factors:List of 2
.. .. .. ..$ means: Named num [1:100] 3.61 3.7 2.76 4.3 2.87 ...
.. .. .. .. ..- attr(*, "names")= chr [1:100] "1" "2" "3" "4" ...
.. .. .. ..$ sds : NULL確認すると分かるのですが、このオブジェクトの中身はtrainつまり学習データそのものです。ベーシックな協調フィルタリングは、データをモデル化をしているわけではなく、すべての学習データを保持しているだけなのです。predict関数を実施する時に初めてレコメンド対象ユーザと保持している学習用ユーザすべての距離の組み合わせを計算し、推定します。協調フィルタリングは、このような仕組みのためどうしても処理コストがかかってしまいます。
今回はユーザベース協調フィルタリングをスクラッチで実装してみました。シンプルなロジックですが、実装する際に検討すべきポイントが、それなりに多いことをおわかりいただけたと思います。ですが、今回の実装だと、速度面も含め改善の余地が大いにありそうです。
次回は、レコメンデーションの評価指標について触れ、モデルの評価・改善、協調フィルタリング以外の手法との精度比較を行いたいと思います。 それではごきげんよう。
あなたにオススメの記事

2023.12.01
生成AI(ジェネレーティブAI)とは?ChatGPTとの違いや仕組み・種類・活用事例

2023.09.21
DX(デジタルトランスフォーメーション)とは?今さら聞けない意味・定義を分かりやすく解説【2024年最新】

2023.11.24
【現役社員が解説】データサイエンティストとは?仕事内容やAI・DX時代に必要なスキル

2023.09.08
DX事例26選:6つの業界別に紹介~有名企業はどんなDXをやっている?~【2024年最新版】

2023.08.23
LLM(大規模言語モデル)とは?生成AIとの違いや活用事例・課題

2024.03.22
生成AIの評価指標・ベンチマークとそれらに関連する問題点や限界を解説

