メルマガ登録

「強化学習入門」の第2弾。今回は、強化学習の手法の一つ「Policy Gradient」について解説しています。加えて、「Policy Gradient」でTensorflow, Keras, OpenAI Gymを使ったCart Poleの実装内容もご紹介しています!
こんにちは、AI開発部の高橋です。今回は強化学習の手法の一つであるPolicy Gradientを説明します。そしてTensorflow, Keras, OpenAI Gymを使ってCartPoleを実装してみます。
強化学習が初めての方は、こちらの入門編を先に読むことをオススメします。
【関連記事】強化学習入門 ~これから強化学習を学びたい人のための基礎知識~
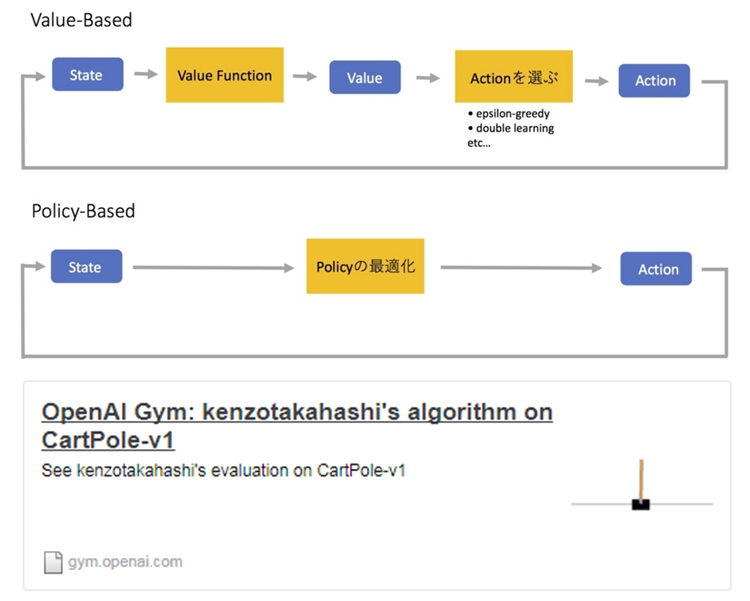
強化学習のアルゴリズムには、大きく分けてValue-BasedとPolicy-Basedの2つがあります。入門編ではValue-Basedについて解説をしています。
では、今回ご紹介するPolicy-BasedはValued-Basedと何が違うのでしょうか?
下記の図は、それぞれのアルゴリズムのフローを表しています。青いボックスは値、黄色いボックスは関数のようなものです。
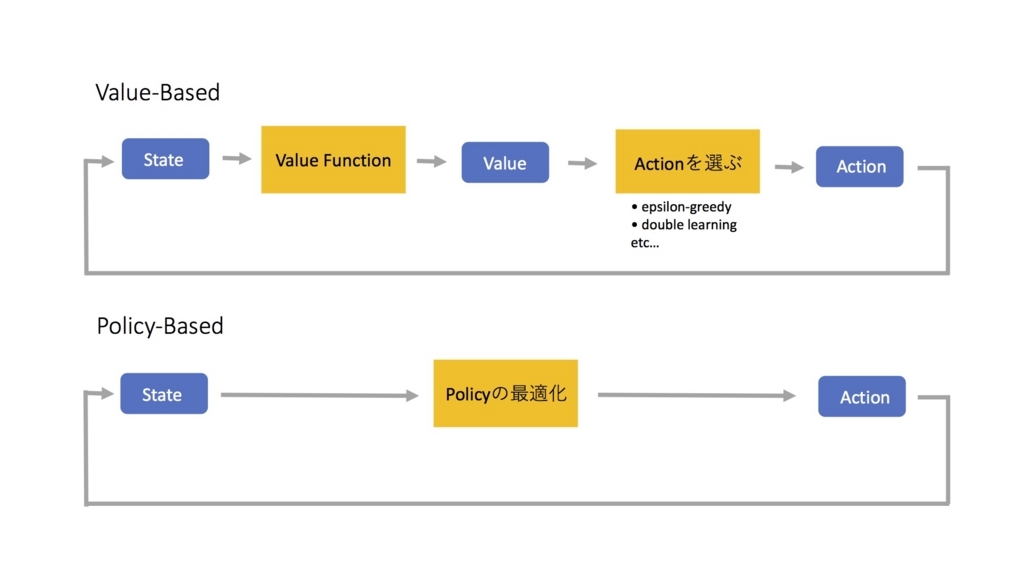
上記をご覧いただくと、Policy-Basedの方がValue-Basedよりもシンプルな構造となっているのがわかります。
※Policy-BasedのアルゴリズムはすべてPolicy Gradientの派生なので、このブログではPolicy-BasedとPolicy Gradientを同じような意味で使っています。
それでは、Policy Gradientがどのようなところで使われているかを、軽くご紹介します。
強化学習で有名なアプリケーションといえば、AlphaGoとAtari Gameです。
AlphaGoでは、まず教師あり学習でプロのプレイを学習させ、その後Policy Gradientを使って自分自身と勝負することによって、さらに強くなっています。
Atari Gameは元々はDeep Q-Network(DQN)というValue-Basedを使っていたのですが、現在はAsynchronous Advantage Actor-Critic(A3C)というPolicy-BasedとValue-Basedを両方使ったアルゴリズムが主流です。
Value-Basedはもう要らないのかというと決してそんなことはなく、アプリケーションに応じて適切な手法を使うことが大切です。
Value-Basedでは、まず、あるState(状態)\( s_t\)に対してAction(行動)\( a_t\)を取った時のReturnを計算します。これを計算する関数をValue Functionと呼びます。
Reward, Return, Valueが混乱し易いのでここで定義します。
Reward(報酬)は1ステップ毎にもらえるものです。
Returnは、あるステップからEpisodeが終わるまでのRewardを足したものです。その際\( \gamma\)を使って直近のRewardに重みをつけることもあります。例えば\( \gamma=.99\)の場合は、nステップ後のRewardに\( .99^n\)を掛けます。
Value(価値)はReturnの予測です。
Episodeを重ねるうちに、State, Action, Returnのデータが溜まっていき、より正確なReturnをValueとして予測できるようになります。
ここまではValue-Basedの前半部分の話です。後半のValueからActionを選ぶ部分でも、幾つかの手法があります。当然Returnが高いActionを選ぶべきなのですが、データが少なく正確なReturnが分からない初期段階でその戦略をとると、Explore(探索)をせず他のActionを全く試さなくなります。なので、何割かの確率でランダムにActionを選択することによってなるべく多くのStateとActionの組み合わせを試すようにします。これがEpsilon-Greedyという手法です。他にもDouble Learningの様に、Actionの選択自体を強化学習で最適化する高度な手法もあります。
まとめると、Valued-BasedはValue-FunctionとActionを選ぶ部分の2つのパーツによって、成り立っています。
Value Functionを介してActionを選択するValue-Basedに対して、Policy-BasedはStateから直接最適なActionを予測します。
表記の説明です。
Policy, \( \pi_θ(s, a) \) はState sに対してAction aをする確率です。
State Value, \( V^{\pi_\theta}(s)\) – はState sのValueです。
Action Value, \( Q^{π_θ}(s,a)\) – はState sでAction aを取った時のValueです。
Policy Gradientは最適化のアルゴリズムです。目的関数 J(θ) はStart Valueと呼ばれるもので、初期のState \( s_1\)のValueになります。
$$
J(\theta) = V^{\pi_\theta}(s_1)
\tag{1}
$$
目的関数の勾配は、以下の通りです。これはPolicy Gradient Theoremというものを元にしているのですが、証明は割愛します。詳しくはSuttonの13.2章を参照してください。
$$
\nabla_θ J(θ) = E_{\pi_θ}[\nabla_θlog \pi_θ(s, a) Q^{\pi_θ}(s, a)]
\tag{2}
$$
それではPolicy GradientでCartPoleを解くエージェントを実装してみましょう。
完成版のGistはこちらを見てください。
CartPoleではStateの変数が4つ(カートの位置、カートの速度、ポールの角度、ポールが傾く速度)あるので、Stateはこれらの組み合わせで成り立っています。
Actionは右に動くか左に動くかの2種類です。
CartPoleはある角度までポールが傾くか、エリア外までカートがはみ出てしまったらそのEpisodeが終了となります。RewardはEpisodeが終了するまで1回のステップに対して1もらえます。つまり、Actionを10回行ってEpisodeが終了したら得られるRewardの合計は10です。
Python3.5.1, tensorflow1.2.1, keras2.0.6, gym0.9.2を使っています。
https://gym.openai.com/envsには、CartPole-v0とCartPole-v1があります。違いは、CartPole-v0ではRewardが200になると強制的にEpisodeが終了し、CartPole-v1では500で終了することです。今回はv1を使います。
import collections
import gym
import numpy as np
import tensorflow as tf
from keras.models import Model
from keras.layers import Input, Dense
from keras.utils import to_categorical
env = gym.make('CartPole-v1')
NUM_STATES = env.env.observation_space.shape[0]
NUM_ACTIONS = env.env.action_space.n
LEARNING_RATE = 0.0005次に、Policy \( \pi_\theta\)の最適化を行うモデルのクラスを書きます。\( \pi_\theta\)は、ニューラルネットワークでモデル化します。
Kerasでニューラルネットワークのモデルを書き、_build_graphでtensorflowを使ってlossやoptimizerを設定します。
1サンプル毎にモデルをアップデートするので、(2)の期待値の\( E\)を外し\( Q^{\pi_\theta}(s_t,a_t)\)のサンプル\( v_t\)を使います。\( \alpha\)はlearning rate です。
$$
\Delta\theta_t = \alpha\nabla_\theta log \pi_\theta(s_t, a_t) v_t
\tag{3}
$$
一般的な教師あり学習と違い、Policy Gradientでは目的関数の\( J(θ)\)を最大化する必要があります。しかしtensorflowにmaximizeはないので、マイナスを付けてlossの扱いとします。
Tensorflowがminimizeで勝手に勾配を計算してくれるので、勾配を外します。
$$
L_t = -\alpha log \pi_\theta(s_t, a_t) v_t
\tag{4}
$$
log_probが\( log \pi_\theta(s_t, a_t)\)で、targetが\( v_t\)に当たります。
class PolicyEstimator():
def __init__(self):
l_input = Input(shape=(NUM_STATES, ))
l_dense = Dense(20, activation='relu')(l_input)
action_probs = Dense(NUM_ACTIONS, activation='softmax')(l_dense)
model = Model(inputs=[l_input], outputs=[action_probs])
self.state, self.action, self.target, self.action_probs, self.minimize, self.loss = self._build_graph(model)
def _build_graph(self, model):
state = tf.placeholder(tf.float32)
action = tf.placeholder(tf.float32, shape=(None, NUM_ACTIONS))
target = tf.placeholder(tf.float32, shape=(None))
action_probs = model(state)
log_prob = tf.log(tf.reduce_sum(action_probs * action))
loss = -log_prob * target
optimizer = tf.train.AdamOptimizer(LEARNING_RATE)
minimize = optimizer.minimize(loss)
return state, action, target, action_probs, minimize, loss
def predict(self, sess, state):
return sess.run(self.action_probs, { self.state: [state] })
def update(self, sess, state, action, target):
feed_dict = {self.state:[state], self.target:target, self.action:to_categorical(action, NUM_ACTIONS)}
_, loss = sess.run([self.minimize, self.loss], feed_dict)
return loss上記のPolicyEstimatorクラスを使って、学習するためのコードは以下の通りです。action_probsはそれぞれのActionの確率が入った配列です。そこから確率に従ってランダムにActionを選びます。
Episodeが終わったらReturnを計算します。CartPoleでは\( \gamma\)の影響がなかったので\( \gamma=1\)にしています。
def train(env, sess, estimator_policy, num_episodes, gamma=1.0):
Step = collections.namedtuple("Step", ["state", "action", "reward"])
last_100 = np.zeros(100)
## comment this out for recording
env = gym.wrappers.Monitor(env, 'cartpole_', force=True)
for i_episode in range(1, num_episodes+1):
state = env.reset()
episode = []
while True:
action_probs = estimator_policy.predict(sess, state)[0]
action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
next_state, reward, done, _ = env.step(action)
episode.append(Step(state=state, action=action, reward=reward))
if done:
break
state = next_state
loss_list = []
for t, step in enumerate(episode):
target = sum(gamma**i * t2.reward for i, t2 in enumerate(episode[t:]))
loss = estimator_policy.update(sess, step.state, step.action, target)
loss_list.append(loss)
# log
total_reward = sum(e.reward for e in episode)
last_100[i_episode % 100] = total_reward
last_100_avg = sum(last_100) / (i_episode if i_episode < 100 else 100)
avg_loss = sum(loss_list) / len(loss_list)
print('episode %s avg_loss %s reward: %d last 100: %f' % (i_episode, avg_loss, total_reward, last_100_avg))
if last_100_avg >= env.spec.reward_threshold:
break
return何回か学習させてみると、精度にバラツキがあるのがわかると思います。大体600回ほどで平均475点に達します。
Policy Gradientは、分散が高いのが弱点です。それを補うために、Baselineというものを使います。BaselineにはState Value \( V\)が一番良いと言われています。Action Value \( V\)からState Value \( V\)を引いたAdvantage \( A\)を使うことで分散を減らすことが出来ます。
BaselineはA3Cと同じくPolicy-BasedとValue-Basedを両方使った手法です。
$$
\begin{aligned}
A^{\pi_\theta}(s,a) &= Q^{\pi_\theta}(s,a) – V^{\pi_\theta}(s,a) \\ \nabla_\theta J(\theta) &= E_{\pi_\theta}[\nabla_\theta log \pi_\theta(s, a) A^{\pi_\theta}(s, a)]
\end{aligned}
\tag{4}
$$
それでは、早速Baselineを実装してみましょう。
完成版のGistはこちらを見てください。
Policy Estimatorの他にValue Estimatorのクラスを作ります。
class ValueEstimator():
def __init__(self):
with tf.variable_scope('value_estimator'):
l_input = Input(shape=(NUM_STATES, ))
l_dense = Dense(16, activation='relu')(l_input)
state_value = Dense(1, activation='linear')(l_dense)
value_network = Model(input=l_input, output=state_value)
graph = self._build_graph(value_network)
self.state, self.action, self.target, self.state_value, self.minimize, self.loss = graph
def _build_graph(self, model):
state = tf.placeholder(tf.float32)
action = tf.placeholder(tf.float32, shape=(None, NUM_ACTIONS))
target = tf.placeholder(tf.float32, shape=(None))
state_value = model(state)[0][0]
loss = tf.squared_difference(state_value, target)
optimizer = tf.train.AdamOptimizer(LEARNING_RATE_VALUE)
minimize = optimizer.minimize(loss)
return state, action, target, state_value, minimize, loss
def predict(self, sess, state):
return sess.run(self.state_value, { self.state: [state] })
def update(self, sess, state, target):
feed_dict = {self.state:[state], self.target:target}
_, loss = sess.run([self.minimize, self.loss], feed_dict)
return loss学習はプレーンのPolicy Gradientとほとんど変わりませんが、一つだけCartPole用にカスタマイズしている部分があります。
CartPole-v1は500ステップで強制終了するので、500ステップ目のStateがどんなに良くても、500ステップ目からのRewardの合計は1と計算されてしまいます。これでは精確なState Valueを学習するのが、困難です。よって、500ステップに達成しなかった時のデータで、Value Functionをアップデートするようにしました。
def train(env, sess, policy_estimator, value_estimator, num_episodes, gamma=1.0):
Step = collections.namedtuple("Step", ["state", "action", "reward"])
last_100 = np.zeros(100)
# comment this out for recording
env = gym.wrappers.Monitor(env, 'cartpole_', force=True)
for i_episode in range(1, num_episodes+1):
state = env.reset()
episode = []
while True:
action_probs = policy_estimator.predict(sess, state)[0]
action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
next_state, reward, done, _ = env.step(action)
episode.append(Step(state=state, action=action, reward=reward))
if done:
break
state = next_state
loss_p_list = []
loss_v_list = []
failed = len(episode) < 500
for t, step in enumerate(episode):
total_return = sum(gamma**i * t2.reward for i, t2 in enumerate(episode[t:]))
baseline_value = value_estimator.predict(sess, step.state)
advantage = total_return - baseline_value
# Update our value estimator. Only update it when the episode failed to use only the accurate value.
if failed:
loss_v = value_estimator.update(sess, step.state, total_return)
loss_p = policy_estimator.update(sess, step.state, step.action, advantage)
loss_p_list.append(loss_p)
loss_v_list.append(loss_v)
total_reward = sum(e.reward for e in episode)
last_100[i_episode % 100] = total_reward
last_100_avg = sum(last_100) / (i_episode if i_episode < 100 else 100)
avg_loss_p = sum(loss_p_list) / len(loss_p_list)
avg_loss_v = sum(loss_v_list) / len(loss_v_list)
print('episode %s p: %s v: %s reward: %d last 100: %f' % (i_episode, avg_loss_p, avg_loss_v, total_reward, last_100_avg))
if last_100_avg >= env.spec.reward_threshold:
break
returnBaselineの場合もやはりバラツキはありますが、450回ほどで平均475点に達するので、プレーンのPolicy Gradientより精度が良いです。
今回のブログでは、Policy Gradientの基礎を紹介しました。Value-Basedに比べて理解するのは難しいですが、構造自体は非常にシンプルですし、コードも短いです。Policy-Basedの手法は、他にもA3C, Deterministic Policy Gradient, Trust Region Policy Optimizationなどたくさんあり、これからもさらに増えていくと思います。
あなたにオススメの記事

2023.12.01
生成AI(ジェネレーティブAI)とは?ChatGPTとの違いや仕組み・種類・活用事例

2023.09.21
DX(デジタルトランスフォーメーション)とは?今さら聞けない意味・定義を分かりやすく解説【2024年最新】

2023.11.24
【現役社員が解説】データサイエンティストとは?仕事内容やAI・DX時代に必要なスキル

2023.09.08
DX事例26選:6つの業界別に紹介~有名企業はどんなDXをやっている?~【2024年最新版】

2023.08.23
LLM(大規模言語モデル)とは?生成AIとの違いや活用事例・課題

2024.03.22
生成AIの評価指標・ベンチマークとそれらに関連する問題点や限界を解説

