メルマガ登録

こんにちは。アナリティクスサービス本部の兵藤です。
ブレインパッドのミッションは、 お客様が保有しているデータをビジネス上の価値に変えていくことです。お客様の課題を解決するために、データサイエンティストは業務の中で予測や最適化、最近だと深層学習などのさまざまな技術を駆使しています。
とはいえ、せっかく自分たちが持っている技術でもあるので、社内の業務効率化などにも積極的に活用しています!
本日は「社内での活用事例」として、アナリティクスサービス本部で実施している1on1コーチングの組み合わせを最適化の問題として解き、社内業務を効率化した事例をご紹介します。

私が所属するアナリティクスサービス本部では、「1on1コーチング」という制度を新たに開始しました。
これまでも、マネージャーとメンバー間で1on1ミーティングは行われていましたが、
①弊社のデータサイエンティストには様々な強みを持つ人がいること
②データサイエンティストにも色々な成長パターンがあること
から、各メンバーは上司に拘らず「この人に自分のキャリアを相談したい!」という人を自分で選び、コーチングを受けられる点が「1on1コーチング」の特徴です。
具体的には、まず対象となる社員を「キャリア相談をするメンバー(以降、メンバーと表現します)」と「キャリア相談を受ける側のメンバー(以降、コーチと表現します)」に分けます。次に、メンバーに「1on1をお願いしたいコーチを全て選択してください」というアンケートをWEBで実施し、その結果をもとにその人のコーチを決定します。その後、マッチングしたメンバーとコーチの間で定期的に1on1を実施していきます。1on1では「自分の目指したいキャリア」や「目指す姿になるためにどんなアクションが必要なのか」を会話することで、自分のキャリアについてしっかりと考えるきっかけを提供することを目指しています。
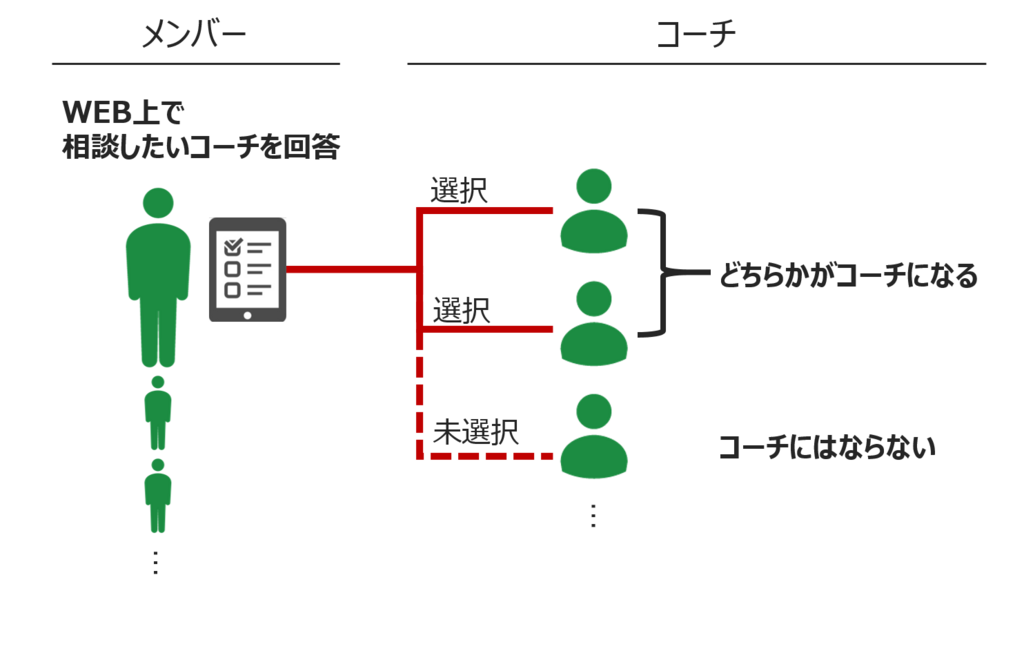
相談をするメンバーは40人、コーチは20人ほどです。このマッチングは、以下のような要件を満たす必要がありました。
① 「相談できないメンバー」が発生し、孤立してしまうのは避けたい。(最優先)
② メンバーが選択したコーチの範囲で、マッチングを実現させたい。
③ コーチはメンバー2人まで持担当できる。(3人以上だと他の業務に支障が出やすくなるので)
④ メンバーはコーチを1人だけ持つ。(1人のメンバーを複数人のコーチが担当することは避ける)
メンバーは複数のコーチ候補を選択できるのでマッチング可能なメンバー・コーチの選択肢は多岐に渡ります。人数が少なければ簡単に考えられそうですが、メンバー40人・コーチ20人となると人間が組み合わせを考えるのはちょっと大変そうです…。
人がやるべきでない大量かつ複雑な作業は機械(アルゴリズム)にやってもらおう、ということで数理計画問題の枠組みで組み合わせを出すことにしました!
今回のマッチングは、最適化の典型的な問題の1つである「0-1ナップサック問題」と捉えることができます。
イメージしやすくするために、簡単な例を挙げながら説明します。1kgまで入るレジ袋に以下の果物を、できるだけ合計金額を高くするように入れることを想定してください。それぞれの果物は1個ずつしかないとします。
| 果物 | 価格 | 重さ(g) |
|---|---|---|
| りんご | 150 | 300 |
| バナナ | 120 | 280 |
| ぶどう | 140 | 270 |
| もも | 200 | 200 |
| メロン | 500 | 600 |
全部入れるとレジ袋が溢れてしまいますので、合計金額が高くなるようにレジ袋に入れる果物、入れない果物を選択しないといけません。このように、各変数について「選択しない(=0)」「選択する(=1)」の最適な選択を求める問題が「0-1ナップサック問題」というものです。
今回のコーチングのお題だと、上の例のレジ袋が「コーチ」で、果物が「メンバー」ですね。コーチには担当できる人数が2人までという制約や、コーチは自身を選択したメンバーしか担当できない、という制約の中でメンバーとコーチの関係を「成立するか」「成立させないか」の最適な選択を算出することになります。
どんな問題かがある程度わかったところで、早速問題を解いていこうと思います。一般的に、最適化問題を解く時は、以下のような流れで解いていきます。途中、数式やコードなど出てきますので、苦手な方は適宜読み飛ばしてください。
基本は「問題を明確にして」「数式にして」「その数式をコードにして機械に計算させる」という流れになります。それでは、詳細を見ていきましょう。
まずは、解きたい問題の確認が必要です。最適化するときは、ここが一番の肝となる部分です。制約条件を見逃したり間違った形で解釈した結果、想定したものと異なる結果になってしまう可能性があるので、注意が必要です。
目的の確認:何を最大化 もしくは最小化したいのか?
制約の確認:各変数にどんな制約を加えないといけないか?
今回のマッチングでいうと、目的は「マッチングしたメンバー数の最大化」となり、制約は以下の3つと考えられます。
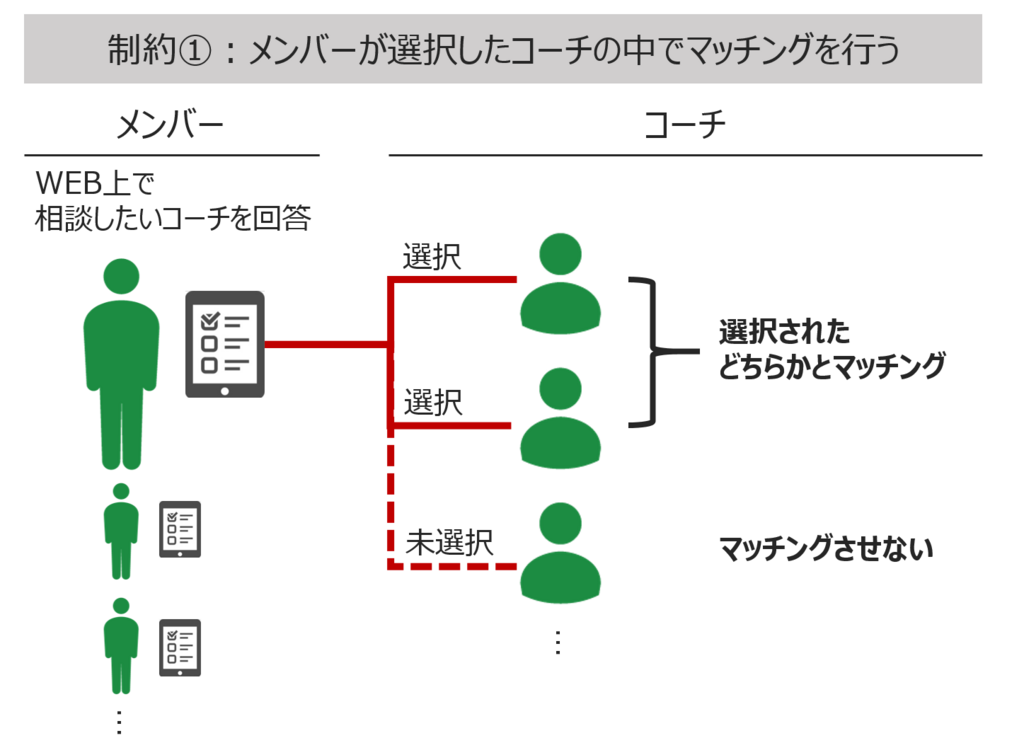
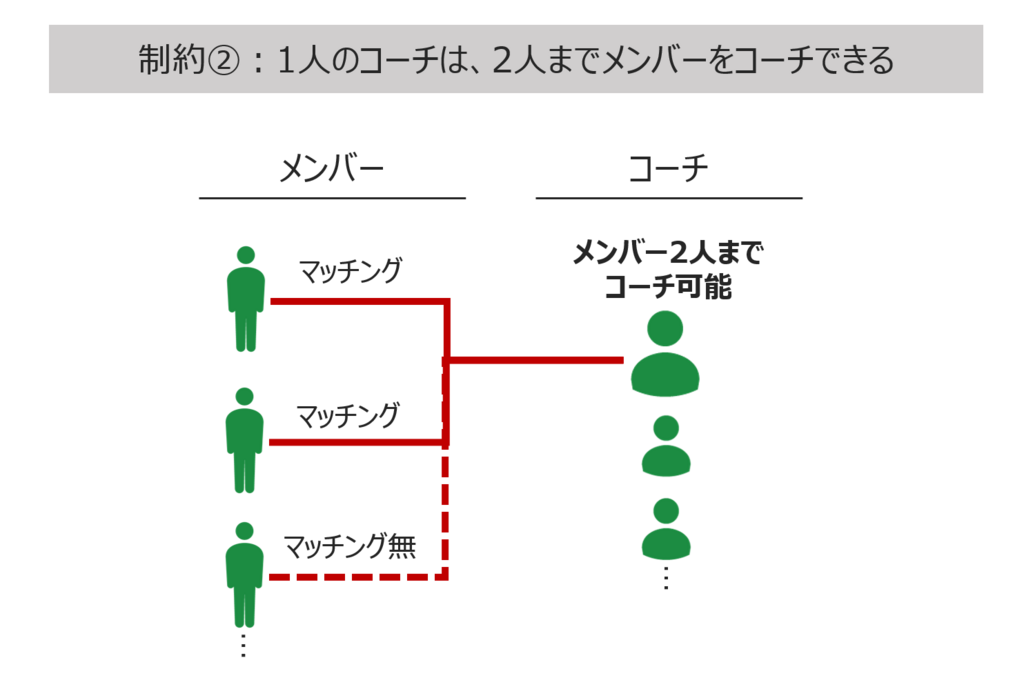
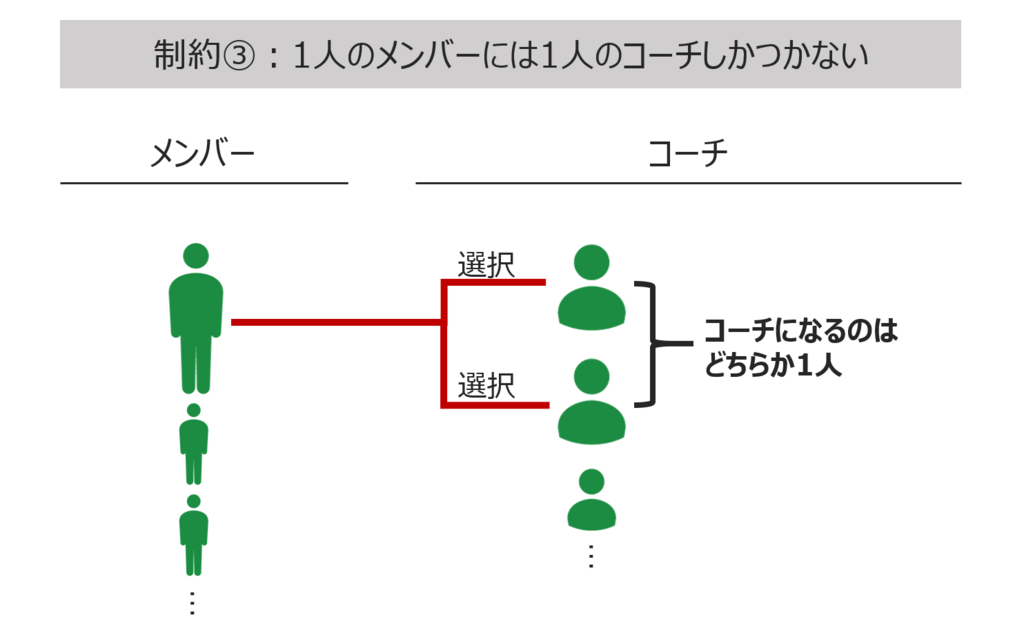
最終的にコードで表現するためには、上記で表現した目的や制約を数式の形で表現する必要があります。例えば今回であれば、以下のように数式にできます。(苦手な方は飛ばしてください)
メンバーの集合を\({ Member = {1, 2, …, m}}\)とする。
コーチの集合を \({ Coach={1, 2, …, n}}\)とする。
「メンバー」と「メンバーが選択(pick)したコーチ」の組の集合を\({ Pick={(1,2), (2,1),…(i,j) \; | Member_{i} \; \mathrm{pick} \; Coach_{j} }}\)とする。
\({Member_i}\)が \({Coach_j}\)とマッチングしなかった場合0、マッチングした場合に1となる0-1変数を\({Match_{ij} \in {0,1}}\)とする。このとき、マッチング数の最大化は以下のように表現できる。
$$
{\sum_{i=1}^{m}\sum_{j=1}^{n} Match_{ij}}
$$また、満たす制約は、それぞれ以下のように表現できる。
制約1:メンバーが選択(pick)したコーチの範囲でマッチングが発生する可能性がある
(選択されていないコーチはマッチングが発生し得ない)$$
{Match_{ij} = 0 \;\;\;\; ∀\,(i,j) \notin Pick}
$$制約2:1人のコーチは、2人までメンバーをコーチできる
$$ {\sum_{i=1}^{m} Match_{ij} \leq 2 \;\;\;\; ∀\,j \in Coach} $$制約3:1人のメンバーには1人のコーチしかつかない
$$
{\sum_{j=1}^{n} Match_{ij} \leq 1 \;\;\;\; ∀\,i \in Member}
$$
いよいよ、定義した数式をコード化し、Pythonのpulpモジュールで実際に解いてみます。(コードを記載していきます。)
まずは必要なモジュールをインポートします。PandasはPythonでデータを「データフレーム」という加工しやすい形に変えた上でさまざまな加工を行うことができるモジュール、pulpは数理最適化問題を解くためのモジュールとざっくり捉えてください。pulpの使い方は、詳しく解説するともう1本記事ができ上がる位の文面を割く必要がありそうなので、本ブログでの詳細な説明は省略させていただきますが、使い方が詳しく紹介されているページ*1がありますので、興味のある方はご参照ください。
import pandas as pd
import pulp as ppまず、テスト用のデータを作成します。
data = pd.DataFrame([[0, 1, 0],
[1, 0, 0],
[0, 1, 0],
[0, 0, 1],
[1, 0, 1],
[1, 1, 0]],
columns=['コーチ1','コーチ2','コーチ3'],
index=['メンバー1','メンバー2','メンバー3','メンバー4','メンバー5','メンバー6']
)
print(data)作成したデータは、以下のとおりです。
「1」は、メンバーが「この人をコーチにしてほしい」と選択したことを表しており、「0」はメンバーがそのコーチを選択しなかったことを表しています。
コーチ1 コーチ2 コーチ3
メンバー1 0 1 0
メンバー2 1 0 0
メンバー3 0 1 0
メンバー4 0 0 1
メンバー5 1 0 1
メンバー6 1 1 0ここから、最もマッチングの合計数が高くなる組み合わせを求めるためのコードを、記載します。
まず問題を定義します。「LpProblem」で問題の名前と、目的関数を最小化(LpMinimize)するか最大化(LpMaximize)するかを、選択します。今回はマッチング数の最大化なので、「LpMaximize」ですね。
# 問題の定義
problem = pp.LpProblem("matching", pp.LpMaximize)次に、最適化で使用する変数を作成します。
変数は「LpVariable」内で変数名、変数の範囲、変数の種類(連続値・整数・2値変数)を定義し、作成します。今回は、定式化で定義した0-1のマッチング変数を作成するので、「LpBinary」と設定してます。
# マッチング変数の作成
match = {}
comb = []
not_pick = []
member = len(data)
coach = len(data.columns)
for m_num in range(member):
for c_num in range(coach):
# 組み合わせ全体
comb.append((m_num, c_num))
if data.iloc[m_num, c_num] == 0:
# 選択されなかった組み合わせの全体(後ほど、制約を作る際に使用します)
not_pick.append((m_num, c_num))
for (m_num, c_num) in comb:
# メンバーとコーチの組み合わせの全体集合
match[m_num, c_num] = pp.LpVariable("match(%s,%s)" % (m_num, c_num), cat=pp.LpBinary)次に、制約条件を作成します。先ほど定義した問題のオブジェクト(problem)に、「+=」の形で制約式を追加することで、制約を設定できます。制約式には、引数で名前をつけることができます。
## 制約1:メンバーが選択したコーチの中でマッチングする(選択のないメンバーはマッチングしない)
for (m_num, c_num) in not_pick:
problem += match[(m_num, c_num)] == 0, "not_pick(%s,%s)" % (m_num, c_num)
## 制約2:コーチが担当できるメンバーは2人まで
for c_num in range(coach):
problem += (pp.lpSum(match[m_num, c_num] for m_num in range(member)) <= 2, "c_(%s)" % (c_num))
## 制約3:1人のメンバーに複数人コーチはつかない
for m_num in range(member):
problem += (pp.lpSum(match[m_num, c_num] for c_num in range(coach)) <= 1, "m_(%s)" % (m_num))最後に、最大化する関数を作成します。これも先ほどの制約の追加と似ていて、最大化する式を作成し問題オブジェクト(problem)に追加することで、設定することができます。
## 目的変数:メンバーとコーチのマッチング合計数
objective = pp.lpSum(match[m_num, c_num] for (m_num, c_num) in match)
problem += objective全ての条件がそろったので、解を求めて結果を出してみましょう。定式化まで正しく行えていれば、中身の解き方まで人が考えなくともpulp内のアルゴリズムが解いてくれます。(ただし制約が厳しすぎる場合は解が無いこともあります。)
# 求解
status = problem.solve()
# 結果の表示
print('メンバー', len(data), '人中', objective.value(), '人がマッチングされました')
for (m_num, c_num) in match:
if match[m_num, c_num].value() == 1:
print('{}さんと{}さんがマッチング!'.format(data.index[m_num], data.columns[c_num]))結果は、こんな感じで表示されます。
全員がちゃんとマッチングしていますし、制約条件も守られていることが確認できると思います。
メンバー6 人中 6.0 人がマッチングされました
メンバー1さんとコーチ2さんがマッチング!
メンバー2さんとコーチ1さんがマッチング!
メンバー3さんとコーチ2さんがマッチング!
メンバー4さんとコーチ3さんがマッチング!
メンバー5さんとコーチ3さんがマッチング!
メンバー6さんとコーチ1さんがマッチング!実際に社内でマッチングロジックを試してみたところ、ちゃんと制約を満たしながらメンバーが全員マッチングする組み合わせを、すぐに見つけてくれました。とても便利です!
ただし、実際の利用シーンでは人の入れ替わりによってコーチ・メンバーを変更させたり、希望者は半年に1回程度新しい組み合わせを試してみたり、と完全に業務に適用するためにはもう少し改善が必要です。今回書いたコードで完結ではなく、これからも随時機能を追加することで、さまざまな状況に対応できるマッチングの仕組みを整えていく予定です!
今回の事例は1on1のマッチングしか利用できないことはなく、もう少し複雑な制約や、新しい変数を導入することで、多くのことに活用できると思います。例えば、今回の事例をさらに発展させる案として、1on1の満足度アンケートや各メンバー・コーチの得意分野も踏まえて、マッチングスコアを定義し、メンバー・コーチの満足度が最大化するマッチングを実現させることが、できるかもしれません。
また、人事系の取り組み以外にも、さまざまなサービスに応用できると思います。例えば法人営業において、成約数を最大化するためにどの営業の方がどの企業を担当するのかのマッチングや、結婚・お見合いなどのマッチングビジネスにも活用できるかもしれません。
いかがだったでしょうか。今回は一風変わって、「自社の業務」を最適化した例をご紹介しました。私以外にも、例えば社員の顔写真を画像認識して似ている顔を分類してみるなど、社内のデータを活用した面白い取り組みの実施例は数多く挙げられます。お客様とのプロジェクトを進める時間以外は、このような形で自己研鑽ができ、またそのような研鑽が推奨される文化であることは、データサイエンティストとしてはとても有り難い環境だと感じています。
本ブログで、ブレインパッドって社内、社外問わずデータ活用を推進できる会社なんだな、なんだか面白そうだな、と思っていただけたら幸いです!
ブレインパッドやデータサイエンティスト職に興味のある方は、ぜひご応募ください!
http://www.brainpad.co.jp/recruit/
あなたにオススメの記事

2023.12.01
生成AI(ジェネレーティブAI)とは?ChatGPTとの違いや仕組み・種類・活用事例

2023.09.21
DX(デジタルトランスフォーメーション)とは?今さら聞けない意味・定義を分かりやすく解説【2024年最新】

2023.11.24
【現役社員が解説】データサイエンティストとは?仕事内容やAI・DX時代に必要なスキル

2023.09.08
DX事例26選:6つの業界別に紹介~有名企業はどんなDXをやっている?~【2024年最新版】

2023.08.23
LLM(大規模言語モデル)とは?生成AIとの違いや活用事例・課題

2024.03.22
生成AIの評価指標・ベンチマークとそれらに関連する問題点や限界を解説

