【連載②】パラメータを自動調整する深層距離学習 -Adacos-【不良品検知ブログ】

距離（Metric）と異常検知

距離（Metric）とは

まず、Metricについてですが、よく距離や計量などと和訳され、”ある二つのデータ間の距離”を意味します（以降ではMetricを距離と表記します）。もし、データ間の距離を適切に測ることができれば、距離が近い同士のデータをまとめていくことでクラスタリングができたり、他のいずれのデータ要素からも距離が遠いデータを異常と判定することで異常検知をしたりと色々と便利です。有名な距離を用いたクラスタリングの手法として、K-meansやk近傍法（k-Nearest Neighbor）があります。ちなみに距離の定義として、ユークリッド距離やマンハッタン距離などが有名です。

k近傍法を用いた異常検知

距離を用いた簡易的な異常検知の方法として、k近傍法を使った手法を紹介します（クラスタリングの文脈で用いられるk近傍法と異なるため注意）。図1のように2次元空間上にデータがプロットされており、これらのデータの中から異常を検知することを考えます。わかりやすさのため、正常なデータは緑色、異常なデータは赤色で表現していますが、実際にはラベルは不明です。各データについて距離（ユークリッド距離とします）に応じて半径を広げていき、k個の他のデータが円の中に入るまで続けます。すると、密集しているデータ（緑色）の円の半径は小さくなり、ポツンと孤立しているデータ（赤色）の円の半径は大きくなります。ここで、”異常データは正常データとは違う特徴を持ち、離れた位置にプロットされる”という仮説をたてると、孤立しているデータ（赤色）ほど異常の可能性が高くなるため、円の半径の大きさでそのデータの異常”具合”を測ることができそうです。ここで、半径の大きさを異常スコアと定義して異常スコアが閾値より上回ったデータを異常と判定することで、異常検知の仕組みができ上がります。

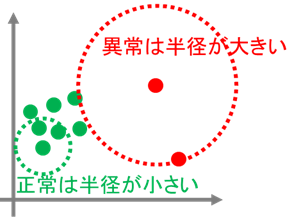
図1の例では、ユークリッド距離を用いることで正常データと異常データを離れた位置関係に置けたため、うまく異常検知ができました。しかし、必ずしもユークリッド距離が適切であるとは限りません。そこで、異常検知のしやすい距離構造（距離関数）を学習することで求めてしまおうというのが、距離学習（Metric Learning）のモチベーションです。

深層距離学習(Deep Metric Learning)とは

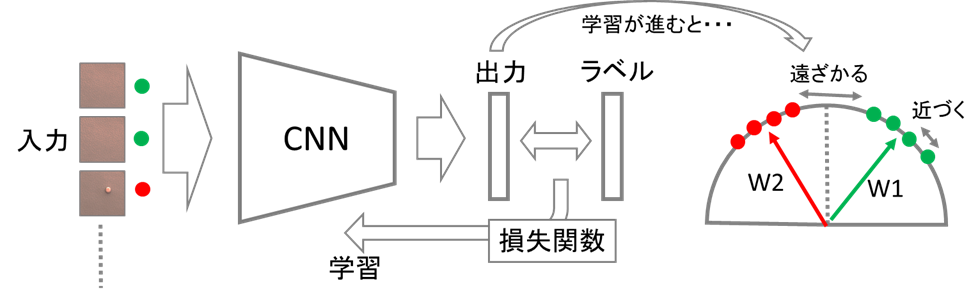
深層距離学習とは、深層学習の特徴抽出の能力を距離学習に取り入れた手法です。深層学習の非線形変換の能力を使うことで、データサイズや次元が大きいデータに対しても異常検知のしやすい距離構造を求めることができます。ラベルが同じデータのペアは近くなり、異なるペアは遠ざかるように損失関数を設計することでネットワークは距離構造を学習できます（図2）。

この損失関数の設計について多く提案されていますが、最近では特にL2 softmax loss*1、CosFace*2、ArcFace*3といった手法が人物認識や顔認識などのタスクで高い分類性能を示すことが報告されています。これらは、コサイン類似度を用いて損失関数を設計することで、出力のベクトルが同一球面上に分布されるように学習させる手法です(図3)。

論文紹介 -AdaCos-

忙しい方のために、AdaCosを2行で説明すると以下のようになります。

• 従来のコサインベースの損失関数を利用した手法（L2 softmax loss、CosFace、ArcFaceなど）に対するパラメータ自動調整機構を提案
• パラメータ調整をした従来手法に対して、同等以上の分類性能を達成

AdaCosについてより知りたいという方は以下の記述をご覧ください。

問題設定、リサーチクエスチョン

AdaCosは顔認識のタスクを想定して提案された深層距離学習手法の一つです。顔認識タスクの難しい点は、顔の向きや撮影時の照明などの要因によって、同じ人物であるにも関わらず特徴が大きく異なる画像を分類しなけらばならないという点です。深層距離学習は、深層学習の高度な特徴量抽出能力により分類がしやすい距離構造を学習することで、先ほど述べた顔認識タスクの問題を解決することができます。特に近年では顔画像間の距離をコサイン類似度を用いて測る手法（L2 softmax loss、CosFace、ArcFaceなど）が分類性能向上に貢献してきました。一方でこれらの手法はハイパーパラメータの値によって性能が大きく変動し不安定という問題も明らかになっています。

この論文では、ハイパーパラメータの値がモデル内の分類器に与える影響を観察することで、分類性能が最も高まる条件を明らかにし、この条件を満たすように学習の度にハイパーパラメータの値を自動調整するアルゴリズムを提案しています。

損失関数とパラメータ\(s, m\)

AdaCosの提案部分はパラメータの自動調整機構であり、損失関数自体は、すでに提案されているArcFaceやCosFace等の損失関数を利用しています。これらの損失関数は、データと各クラスまでの距離を角度で表している点が特徴です。

今回の記事では、ArcFaceの損失関数を用いて説明していきます。図4にArcFaceの全体像を示します。

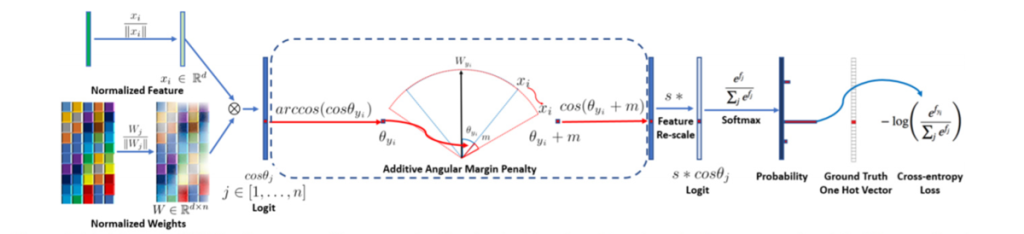
ArcFaceの損失関数は、通常の分類タスクで多く利用されているsoftmax lossをベースにしています。式(1)は、サイズNのミニバッチに対するsoftmax lossを表し、\(i\)がミニバッチ内のイテレーション、\(x\)が出力された特徴量、\(y\)が\(x\)に対する正解ラベル、\(W\)がネットワークの最終層の重みベクトルを意味します。この式は、損失を\(W\)と\(x\)の内積、つまり\(W\)と\(x\)のコサイン類似度に基づいて計算します。

$$L=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{W_{y_{i}}^{T} x_{i}+b_{y_{i}}}}{\sum_{j=1}^{n} e^{W_{j}^{T} x_{i}+b_{j}}} \tag{1} \label{1} $$

ArcFaceでは、softmax lossに二つのパラメータ、スケール[tex:x]とマージン\(m\)を追加した損失関数(2)を用います。なお、\(\theta\)は\(W\)と\(x\)の角度を表します。

$$L=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}} \tag{2} \label{2} $$

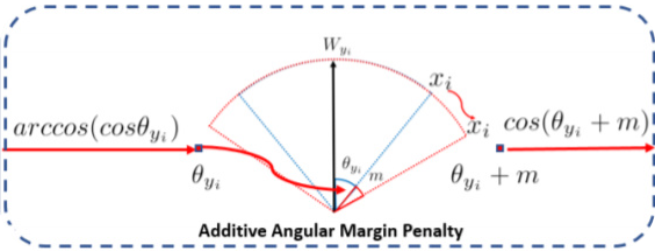
マージン\(m\)を設けることで、正解クラスの重みベクトル\(W_{y_i}\)と\(x_i\)のコサイン類似度を実際より小さく見積り、逆に不正解クラスの重みベクトルとの類似度を大きく見積もります（図5）。つまり、他のクラスの重みベクトルより、\(W_{y_i}\)により近づくように損失を与えることができるため、正解クラスと不正解クラスの重みベクトルを引き離す効果があります。また、スケール\(s\)は、クラス分類確率の分布を調整する効果があります。\(s\)がモデルの学習に与える影響は後述します。

パラメータ\(s\)がモデルの学習に与える影響

ある出力\(x\)の正解クラスに対するクラス分類確率\(P\)と、\(x\)と正解クラスの重みベクトル間の角度\(\theta\)の関係を図6に示します。この図で、\(\theta\)が小さければ、\(x\)と重みベクトルのコサイン類似度が大きくなるため、クラス分類確率\(P\)も大きくなり、逆に\(\theta\)が大きいと、コサイン類似度が小さいため、\(P\)は小さくなる関係が示されています。

図から、パラメータ\(s\)の値によって\(\theta\)と\(P\)の関係の傾きが変化している様子がわかります。ここで、傾きが緩すぎる(\(s=10\))場合、角度\({\theta}=0\)の時でさえ\(P\)が1.0に達しないため、十分にネットワークが出力に自信を持っているにも関わらず、異なる出力をするように損失を与えます。逆に、厳しすぎる(\(s\)=64)場合、角度\(\theta\)のほとんどの範囲で\(P\)が1.0に達するため、ネットワークが自信がない出力に対して損失を与えません。そのため、ネットワークに対して適切な損失を与えるためには、\(s\)が大きすぎず小さすぎないように調整する必要があります。AdaCosは学習中の状況に合わせてパラメータ\(s\)を自動調整することで、最適な学習を実現するアルゴリズムです。

AdaCosの自動調整機構

学習を初めて間もない頃は、\(\theta_{i,y_i}\)はある程度大きな値をとります。効果的にネットワークに損失を与えるためには、パラメータ\(s\)の値を図7の点線のプロットの値に設定すればよさそうです（図7左）。一方、学習がある程度進むと、\(\theta_{i,y_i}\)は小さくなりクラス分類確率がほぼ1.0になるため、点線のプロットではネットワークに損失を与えられません。そこで、損失が与えられるような\(s\)になるよう調整する必要があります（図7右）。

点線のプロットになる[tex:s]の求め方ですが、まず\(\theta_{i, y_i}\)とクラス分類確率\(P\)の関係式を導き、その式の傾きの増減が入れ替わる点、つまり2階微分が0になる\(\theta_{i, y_i}\)が[tex:\pi/4]になる[tex:s]を計算すればよさそうです。

それでは、式(2)中の\(\sum_{k \neq y_{i}} e^{s \cdot \cos \theta_{i, k}}\)を\(B\)とおき、クラス分類確率を以下の式で表します(式(3))。

$$B_{i}=\sum_{k \neq y_{i}} e^{f_{i, k}}=\sum_{k \neq y_{i}} e^{s \cdot \cos \theta_{i, k}} \\
P_{i, y_{i}}=\frac{e^{f_{i, y_{i}}}}{e^{f_{i, y_{i}}}+B_{i}}=\frac{e^{s \cdot \cos \left(\theta_{i, y_{i}}+m\right)}}{e^{s \cdot \cos \left(\theta_{i, y_{i}}+m\right)}+B_{i}} \tag{3} \label{3}$$

今回の記事では説明を省略しますが、パラメータ\(m\)はAdaCosでは用いません。パラメータ\(m\)を無視し、\(P_{i,y_i}\)の2階微分の式を解くことで、\(s\)と\(\theta\)と\(B\)の関係式(4)が求まります。

$$\frac{\partial^{2} P_{i, y_{i}}\left(\theta_{0}\right)}{\partial \theta_{0}^{2}}=0 \\
s_{0}=\frac{\log B_{i}}{\cos \theta_{0}} \tag{4} \label{4} $$

AdaCosはミニバッチごとに\(s\)を調整するため、それに合わせて\(\theta_{i, y_i}\)と\(B_i\)の代替の値を導入します。\(\theta_{i,y_i}\)はミニバッチ内の\(\theta_{i,y_i}\)の中央値\(\theta_{med}\)、\(B_i\)はミニバッチ内の\(B_i\)の平均値\(B_{avg}\)を用います(式(5))。

$$B_{\mathrm{avg}}^{(t)}=\frac{1}{N} \sum_{i \in \mathcal{N}^{(t)}} B_{i}^{(t)}=\frac{1}{N} \sum_{i \in \mathcal{N}^{(t)}} \sum_{k \neq y_{i}} e^{\tilde{s}_{d}^{(t-1)} \cdot \cos \theta_{i, k}} \tag{5} \label{5} $$

以上より、パラメータ\(s\)は式(6)を用いて計算することができます。\(t\)は学習イテレーションを表します。

\(\tilde{s}_{d}^{(t)}=\frac{\log B_{\mathrm{avg}}^{(t)}}{\cos \theta_{\mathrm{med}}^{(t)}} \tag{6} \label{6}\)

• \(\theta_{med}\)が\(\pi/4\), \(\pi/2\)の範囲の時

図7左で示したように、点線のプロットを目指せば十分な損失をネットワークに与えられるので、式(6)の\(\theta_{med}\)の代わりに\(\pi/4\)を用いて\(s\)を求めます。また、\(t=1\)の時の\(B_{avg}\)の初期値ですが、求まらないため推測値\(C-1\)を用います(クラス数をCとおく)。

• \(\theta_{med}\)が\(tex:0\), \(\pi/4\)の範囲の時

図7右で示したように、損失を与えられるsを求めるため、式(6)をそのまま利用します。

これらをまとめて、AdaCosは以下の式に従ってパラメータsを自動調整します(図7)。

$$\tilde{s}_{d}^{(t)}=\left\{\begin{array}{ll}
\sqrt{2} \cdot \log (C-1) & t=0 \\
\frac{\log B_{\text {avg }}(t)}{\cos \left(\min \left(\frac{\pi}{4}, \theta_{\text {med }}^{(t)}\right)\right)} & t \geq 1
\end{array}\right. \tag{7} \label{7}$$

論文の実験結果の一部

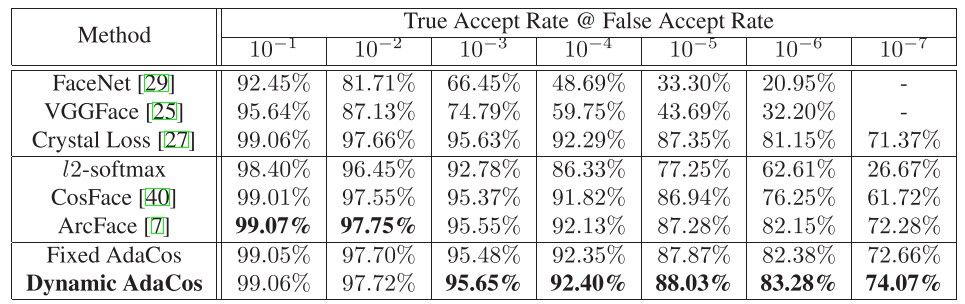
IARPA Janus Benchmark C (IJB-C)*4という1対1の顔認識用データセットに対する提案手法と従来手法のTAR(True Accept Rate)による性能比較の結果を下に載せます(図8)。ArcFaceとAdaCosの黒字で最高性能であることが示されています。注目すべきは、パラメータ調整なしにArcFaceと同等以上の性能を示している点です。AdaCosのこの特徴は、例えば、不良品検知システムに変更があり、モデルの再学習しなければならないといった実案件のケースで調整の手間を省くメリットなどがあります。次の実験で、実案件への応用を念頭に性能検証をしていきたいと思います。

AdaCosの不良品検知の性能検証実験

前置きが長くなりましたが、MVTecADのデータセットを用いて、AdaCosの不良検知の性能検証をします。MVTecADについてはこの連載の初回に記載があるのでそちらを参照してください。実験は以下の実験設定で行います。

実験設定

• モデル
  • CNNはResNet18を採用
  • 入力画像は512×512にリサイズして、グレースケール変換
  • 学習時の画像はランダムに縦横の反転と、サイズの拡大縮小、回転をデータ拡張として適用
  • 2値の教師あり学習モデル
  • 損失関数の出力次元数(クラス数)は20に設定
• データセット
  • MVtecAdの’leather’を使用
  • 複数の不良品クラスを一つに統合
  • 学習データに不良品が含まれていないので、テストデータの不良品を半分移動

学習データは、良品と不良品の枚数が不均衡になっており、不良品の特徴の学習が難しい問題になっています(下図)。

• 評価
  • 残りのテストデータを分割して閾値の探索・検証を実施(3-fold)
• 不良品検知のアプローチ(詳細は後述)
  • k近傍法 (k = 5)による不良品検知
  • クラス分類確率を用いた不良品検知

学習結果

不良品検知の性能を評価する前に、AdaCosの学習が失敗していないか確認をします。

• 学習の様子

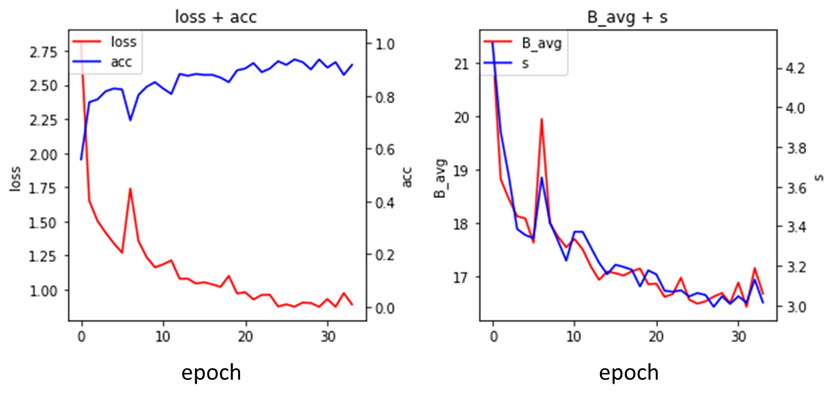
図10に学習データでモデルを学習した際の様子を示します。図10左は、エポック毎の損失(赤)とAccuracy(青)の変化を表します。損失の減少が頭打ちになるまで十分に学習していることがわかります。本来は過学習をしていないか確認するため別途用意した検証データの正解率と比較した方がいいです。図10右は、エポック毎の\(B_{avg}\)(赤)とパラメータ\(s\)(青)の変化を表します。\(s\)とlossを比較すると、初期の\(s\)の急激な減少に合わせてlossも減少していることから、AdaCosの自動調整によりネットワークの学習の最適化が促進されている様子がわかります。

• 学習データの潜在空間上の可視化

tSNEという可視化アルゴリズムを利用して、学習データとテストデータの潜在空間上の位置を可視化しました。学習データの潜在空間では概ね良品と不良品のクラスタを作ることに成功していそうな気がします。一方、テストデータの潜在空間では、良品の集合の中に不良品が少し混ざっており、綺麗なクラスタは作れていませんが、ある程度は良品と不良品の分離はできています。それでは、この特徴量を使って不良品検知を試みてみましょう。

不良品検知の性能検証結果

k近傍法による不良品検知手法とクラス分類確率を用いた不良品検知手法の2手法で性能を評価します。

k近傍法による不良品検知

まずは、単純にk近傍法を用いて不良品検知を試みましょう。記事の冒頭で説明した通りに実行します。テストデータの全ての2ペアについて出力のコサイン距離を求めた後、各データについて、k番目に近いペアの「1 – コサイン類似度」のエクスポネンシャルを異常スコアとします。

3-foldのうち一つの結果を下の図12に示します。検証データを用いてAUCと最適な閾値を求め、閾値を使ってテストデータに対する性能評価をしました。結果をみると、見逃しも誤検知も少ないバランスの良いモデルになりました。上図では、テストデータの潜在空間上の良品と不良品の近傍の距離にあまり差がなく不良品検知は難しいと予想していたため意外でした。異常スコアを求める際にエクスポネンシャルを用いずにスコアの差を出にくくすると、全く性能が出ないため、人間の目にはわからない小さな近傍の距離の差が存在するのだと思われます。

クラス分類確率を用いた不良品検知

AdaCosの損失関数はsoft max lossベースなため、各クラスに対するクラス分類確率を用いて損失を計算します。せっかくなので、このクラス分類確率を取り出して異常検知に利用するアプローチも試してみます。今回は、異常スコアを「1 – 良品クラスに対するクラス分類確率」とします。

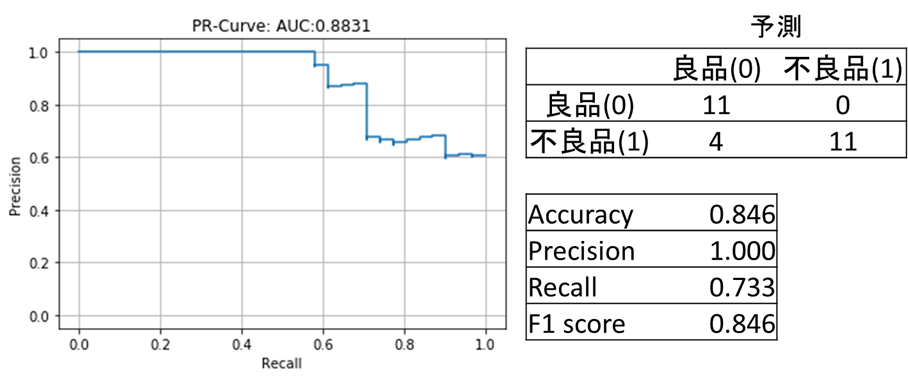
結果(図13)ですが、k近傍のモデルと比較すると、不良の誤検知が0になった代わりに見逃しが少し発生しやすいモデルになりました。とは言え、全体的にk近傍と同程度に高性能な不良品検知モデルと言えるでしょう。不良の見逃しが発生しやすくなった理由ですが、実際には複数ある不良品クラスを一つに統合して学習していることにあるかもしれません。モデルが不良品クラスの分布をうまく捉えられないため、不良品クラス側によった位置に識別境界を引いている可能性があります。

クラス別の不良品検知の性能検証とモデルの重みの可視化

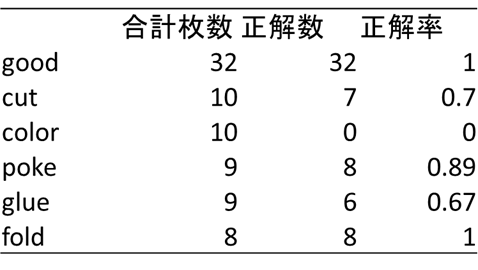
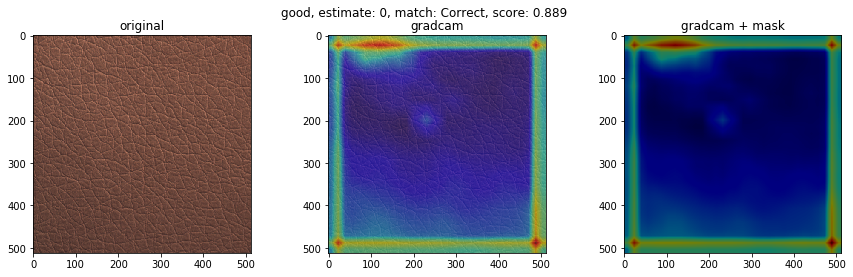
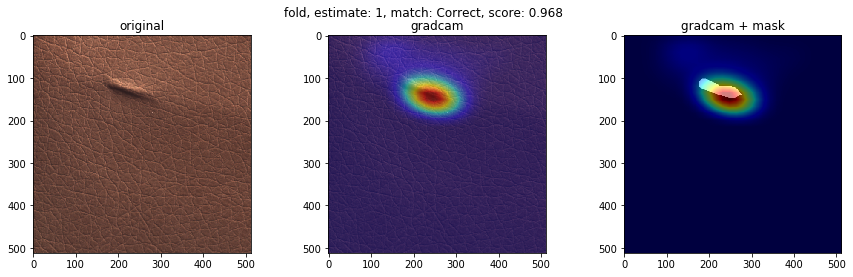
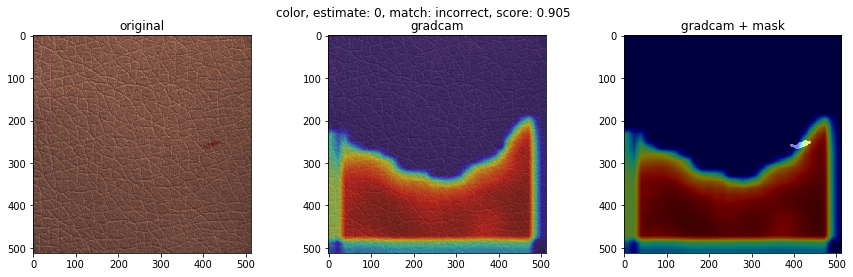
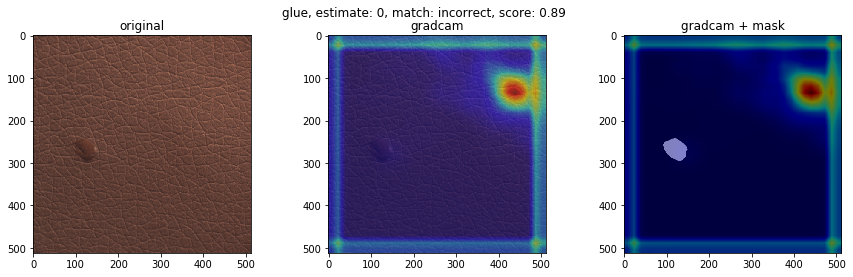
不良品の種類で、検知の得意不得意があるか検証します。テストデータにおけるクラスごとの不良品検知の結果を下図に示します(クラス分類確率を用いた不良品検知モデル)。’good'(良品)、’poke’、’fold’はほぼ検知が成功している一方、’color’は検知に完全に失敗しました。それぞれどのような不良品でしょうか。GradCamによる重みの可視化も合わせてみてみます。

下に、検知が得意なクラスと検知が苦手なクラスの可視化画像を載せます。左から順番に、オリジナル画像、GradCam画像、不良個所を表したマスク画像にGradCam画像を重ねたものを表します。結果より、検知が得意なクラスの不良は、凹凸がわかりやすいことが多く、GradCamの色付けからモデルが不良個所を捉えていることがわかります。一方、検知が苦手なクラスの不良は、色が背景色と似ており、凹凸も少ないことが多く、モデルが不良個所を捉えていない様子がわかります。この結果は、学習させる際に、グレースケール変換をしているのが原因かもしれません。

検知が得意なクラス(good, poke, fold)

まとめ

上記の性能検証実験から、冒頭で述べたようにAdaCosを用いた不良検知手法について実案件への応用を念頭に検証していきます。

パラメータ調整の煩雑さから本当に開放されるのか

AdaCosによって損失関数のパラメータ調整は不要ですが、AdaCosで用いる深層ニューラルネットワーク部分で、ネットワークパラメータやデータ拡張の設定は必要です。今回の検証中、データ拡張の設定で非常に時間がかかりました。そういう意味で、AdaCosがイントロで想定したような ”調整いらずの内製化が容易なアルゴリズム”とは言えないと思われます。

学習速度、検知性能

AdaCosは、効率的に学習を進めるために学習中に自動的にパラメータを調整するアルゴリズムです。そのため、従来の手法より、短い学習速度で高い性能を実現することが期待できます。この性質より、不良品検知の問題設定は変わらず、学習データの追加といった簡単な変更が発生する場合に、従来の手法より早くモデルの再構築が可能です。実際の案件において、例えば、学習データの更新をなるべくはやくモデルの性能に反映させなければならないという要件がある場合に適していると思われます。

不良個所の特定

今回はGradCamという深層学習のネットワークの重みを可視化するアルゴリズムを用いて、不良個所の特定を試みました。今回の検証では、検知の正解率が高い不良についてほぼ正確に不良個所を特定できたため、不良個所の位置も知りたいクライアントに対してその要望に応えられる可能性があります。しかし、あくまで重みの可視化なため、必ずしもGradCamの可視化画像とモデルの不良の判定基準が一致しているとは限らないことに注意は必要です。

結論として、AdaCosは諸々の手動調整なしに不良品検知を実現できるアルゴリズムではありませんでしたが、それでも上で述べたような性質から実際の案件でも利用できる可能性が十分にあります。今回の検証をもとにAdaCosを使った不良品検知手法も検討したいと思います。