特徴量作成方法

本稿で説明するのは、以下に示すBTF論文に登場する5種類の特徴量作成方法です。

• iNet
• Raw
• HOG
• SIFT
• FPFH

ほとんどの特徴量は、2次元画像を対象にしたものですが、「FPFH」のみが3次元データである点群を対象にしています。

iNet（対象：2次元画像）

次の図のように、ImageNetデータセット[ImageNet]で事前学習したResNet系アーキテクチャの中間層から2種類の特徴マップを結合したものを特徴量とする手法です。

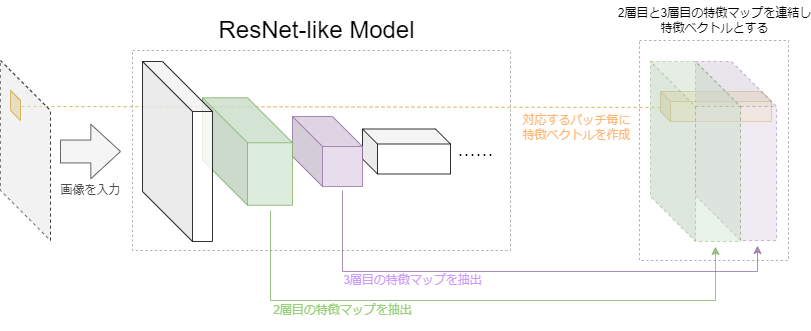
BTF論文では、ResNet系アーキテクチャとして、WideResNet50を利用しています。
留意点として、2次元画像として深度マップを使う場合でもImageNetデータセットで事前学習したモデルを使っています。

Raw（対象：2次元画像）

入力画像のRGB値を、そのまま特徴量として利用します。

HOG（対象：2次元画像）

Histogram of Oriented Gradients (HOG)[HOG]を利用する手法です。

HOGは人物検出のための特徴量として提案されました。
HOG特徴量の性質として、その計算方法から、物体の大きさや回転の変化に弱いですが、物体の平行移動や輝度の変化に強いと考えられます。

計算方法

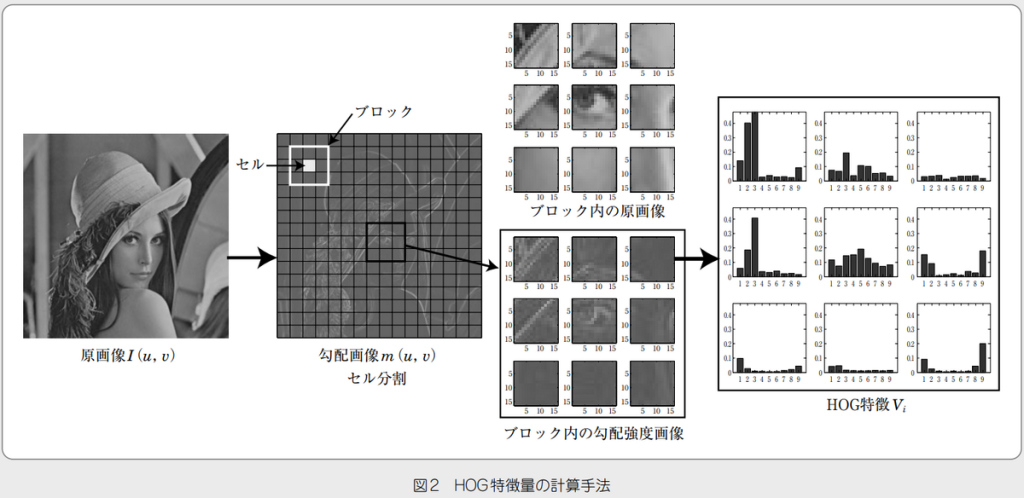
HOG特徴量は、3種類の大きさが異なる領域で計算されます：

• ピクセル 画像を構成する最小単位です。
• セル（cell） 全ピクセルが格子状に分割されたときの構成要素を表します。
  上の画像の例では、16×16ピクセルの大きさのセルに分割されています。
• ブロック（block） 複数の隣接するセルで構成されます。
  上の画像の例では、1つのブロックが9×9個のセルで構成されています。

計算手順は以下の通りです。

1. 各ピクセルで、隣接するピクセルの輝度を使い、画像の輝度に基づく輝度勾配を計算します。
2. 各セル内で、ピクセル毎に計算された輝度勾配について、勾配強度で重み付けした勾配方向のヒストグラムを作成します。
3. 各ブロック内で、セル毎に計算された勾配方向ヒストグラムを、ブロック内で正規化します。
4. 各セルに対応した1次元の勾配方向ヒストグラムを全て結合して、HOG特徴量ベクトルを作成します。

なお、輝度勾配を表す勾配強度\(m\)と勾配方向\(theta\)は以下の式で計算します。

$$\begin{align}
m(u, v) &= \sqrt{\Delta I_u(u, v)^2 + \Delta I_v(u, v)^2} \\
\theta(u, v) &= \tan^{-1} \frac{\Delta I_v(u, v)}{\Delta I_u(u, v)} \\
\end{align}$$

$$\begin{cases}
\Delta I_u(u, v) &= I(u + 1, v) – I(u – 1, v) \\
\Delta I_v(u, v) &= I(u, v + 1) – (u, v – 1)
\end{cases}$$

ここで、画像内のピクセル毎に含まれる輝度\( I(u, v)\)をとして表しており、\(u, v\)はそれぞれが横方向と縦方向のピクセル位置を表す離散的な数字です。

SIFT（対象：2次元画像）

Scale-Invariant Feature Transform (SIFT)[SIFT]を利用する手法です。

SIFTは、異なる地点にあるカメラから撮影された画像間の対応点を求めるための特徴量として提案されました。
SIFT特徴量の性質として、物体の大きさや回転、輝度の変化に強いです。
さらには、異なる角度から撮影されたときに起こりえるアフィン変換に対しても、ある程度ロバストです。

BTF論文中では、Dense Scale-Invariant Feature Transform (D-SIFT)を利用する手法として紹介されています。D-SIFTはSIFTの派生アルゴリズムです。

SIFTは重要であると判定されたいくつかのピクセルについて特徴量計算されるのに対し、D-SIFTはあらかじめ指定しておいた複数ピクセルに対して特徴量計算される特徴があります。

計算方法

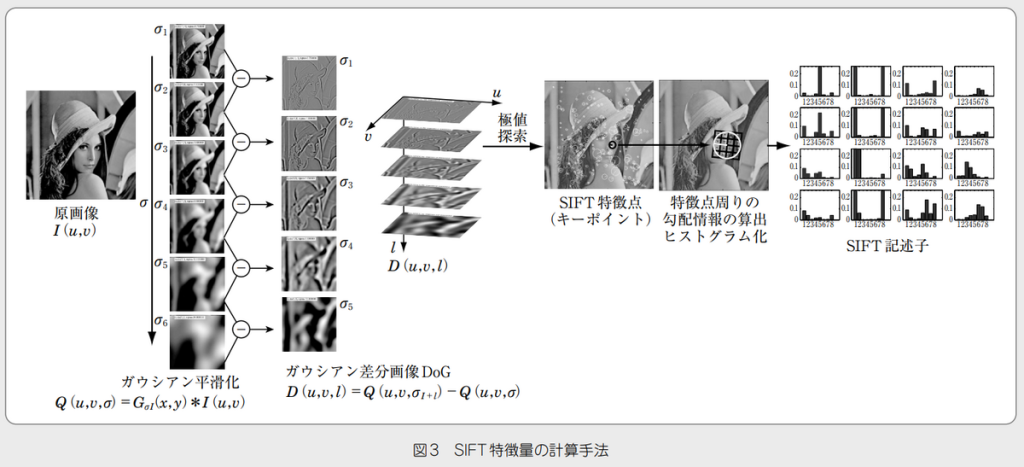
簡単な計算手順は以下の通りです。

1. 入力画像を、k倍ずつ標準偏差\(sigma\)が大きくなるような複数のガウシアンにより順番に畳み込み演算し、複数の平滑化画像\( L(x, y, sigma)\)を作成します。
2. 平滑化画像の差分であるDifference of Gaussian (DoG)と呼ばれる\( D(x, y, sigma) = L(x, y, k sigma) – L(x, y, sigma)\)を求めます。
3. \( D(x, y, sigma)\)について、特徴があると考えられる極値となるピクセルを全て探索します。このときに、極値であるピクセル位置に加え、DoGのスケールによって決まるスケール情報も同時に決まります。

極値であると判定されたピクセル（キーポイント）と周囲のピクセルで計算した輝度勾配より、（HOGの計算方法と同様に）勾配方向ヒストグラムを次図のように計算します。
なお、ヒストグラム作成のために使う周囲のピクセル範囲の決め方は、極値探索のときに求めたスケール情報に基づきます。

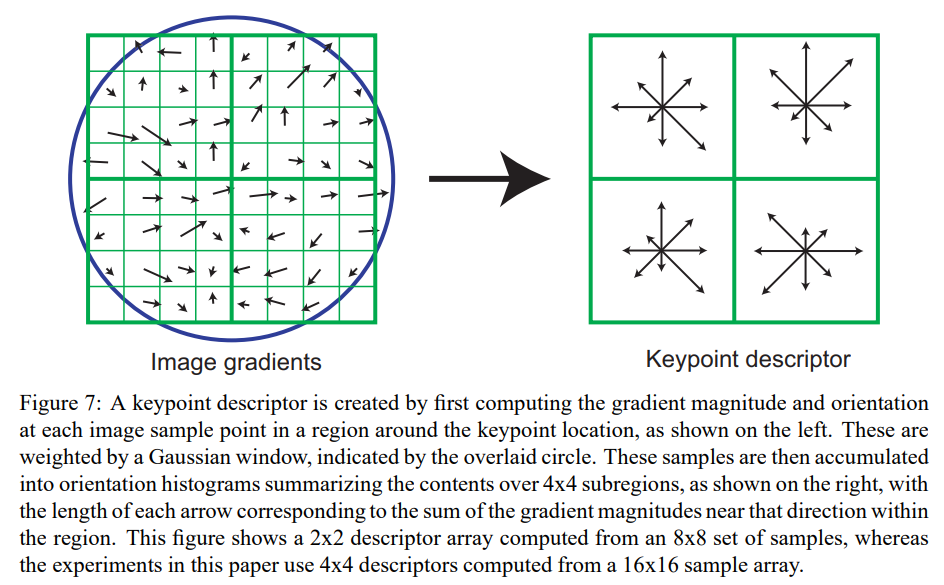
この画像の例に従うと、左図のように元の画像範囲が8×8ピクセルの勾配に対して、右図のように4×4の大きな領域に再分割して各領域で勾配方向ヒストグラムを計算します。

求めた1次元の勾配方向ヒストグラムを全て結合して、SIFT特徴量ベクトルを作成します。

本稿では、輝度や回転などの変化に対してSIFT特徴量がロバストであるための工夫や計算式の意味の説明などについては割愛しました。

興味があれば、SIFT論文[SIFT]を参考にしてください。

FPFH（対象：3次元点群データ）

Fast Point Feature Histograms (FPFH)[FPFH]を利用する手法です。

FPFHは、Point Feature Histograms (PFH)の高速化を目的としており、3次元データの位置合わせのための特徴量として提案されました。

FPFHの対象は、これまで紹介した手法のように2次元画像を対象としておらず、3次元データである点群を対象としています。さらに、各点に法線ベクトルが対応付けられている必要があります。

FPFHを定性的に説明すると、各点について周辺の幾何学的な特徴を捉えるために、近傍点との空間的な位置関係を角度の関係に落とし込み、FPFH特徴量としています。

計算方法

特徴量計算する点\(p_q\)について、近傍点との関係をヒストグラムにします。

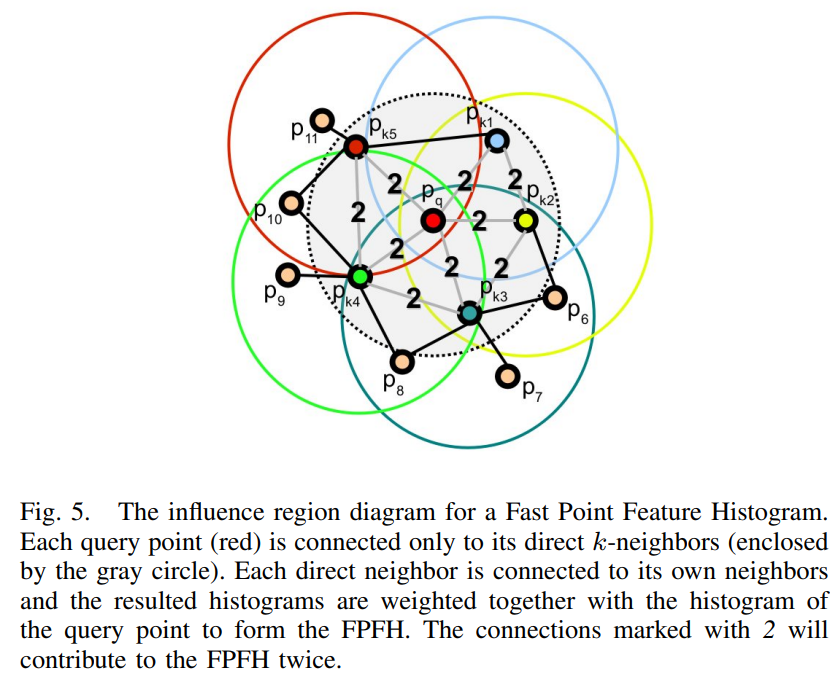
計算手順は以下の通りです。

1. 上図のように、あらかじめ決定しておいた個数分だけ近傍点を探します。
   上図では、灰色の球内に収まる点が近傍点であるとわかりました。
2. 全ての近傍点に対して、基準となる点の座標\(p_q\)や法線ベクトル\(n_q\)と近傍点の座標\(p_i\)や法線ベクトル\(n_i\)の関係を表す3種類の特徴量\(\alpha_i, \phi_i, \theta_i\)を以下の方法で計算し、ヒストグラム\(SPFH(p_q)\)を作成します。
3. 各近傍点\(p_i\)について、上記手順の1.と2.と同じように、新たに近傍点を探索し、ヒストグラム\(SPFH(p_i)\)を作成します。
4. 次の式により、\(p_q\)に対応する特徴量を計算します。なお、\(d_i=p_i – p_q\)です。
   $$\begin{equation}
   FPFH(p_q)=SPFH(p_q) +\ frac{1}{k} \sum_{i=1}^k \frac{1}{\omega_i} SPFH(p_i)
   \end{equation}$$
   この式のように、着目する2点間の位置関係をPFHよりも少なくすることで計算時間が短くなっています。

なお、上記の手順2で説明したSPFH (Simplified Point Feature Histogram)の計算のために必要な3種類の特徴量\(\alpha_i, \phi_i, \theta_i\)の計算方法は以下の通りです。

$$\begin{align}
\alpha_i &= v_i \cdot n_i \\
\phi_i &= \frac{u \cdot d_i}{|d_i|} \\
\theta_i &= \arctan\left( \frac{w_i \cdot n_i}{u \cdot n_i}\right)
\end{align}$$

ここで、\(u, v_i, w_i\)は直行するベクトルであり、以下の式を満たします。

$$\begin{align}
u &= n_q \\
v_i &= d_i \times u \\
w_i &= u \times v_i
\end{align}$$

上式を可視化したものは、以下のようになります。

まとめ

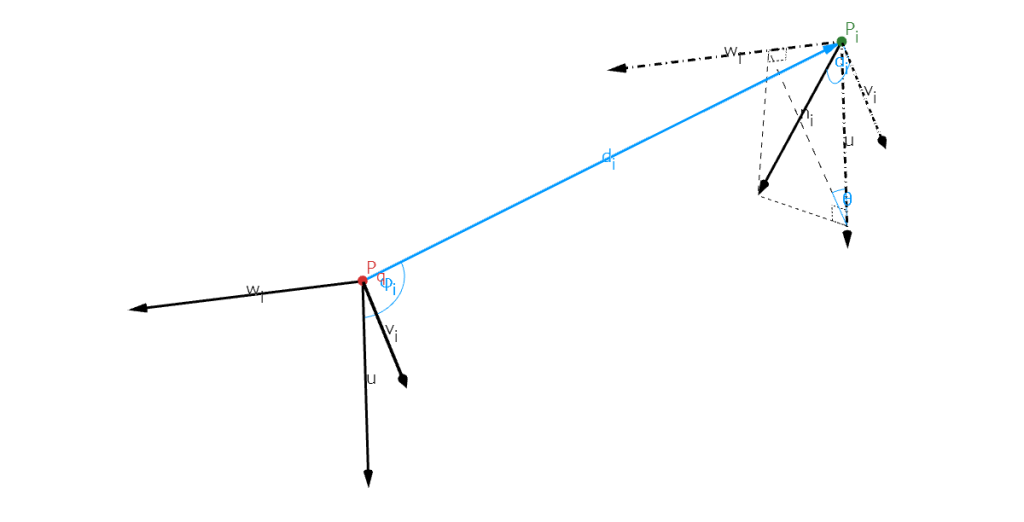
2次元画像や3次元データによる5種類の特徴量作成方法について、BTF論文で紹介されているものに準じて、紹介しました。

各特徴量を使った場合の異常検知精度は、3次元データによる異常検知を目的に作成されたMVTec 3D-ADデータセットにおいて、概ね次の順番で良くなっていることが分かりました： FPFH > iNet > SIFT > HOG > Raw。
さらに、良い精度であったFPFHとiNetの特徴量を結合して新たな特徴量とすることで、より良い精度になることも分かりました。
詳しくは、冒頭でも示しましたが、次のリンクの記事で紹介しています。

ブレインパッドでは、3次元データを扱った手法や異常検知技術をビジネスに活用するため、調査や検証を積極的に実施しています。
本記事を通じて、ブレインパッドの取り組みについて、ご興味を持っていただけますと幸いです。

＜連載記事＞

• 3D異常検知モデルの検証結果：【3D異常検知・本編】3次元データを活用した異常検知方法の検証 – Platinum Data Blog by BrainPad
• 3D異常検知用データセットの紹介：【3D異常検知・補足編】3Dデータによる異常検知用データセットMVTec 3D-ADの紹介 – Platinum Data Blog by BrainPad
• 2D+3D特徴量作成方法：【3D異常検知】2次元画像と3次元データのための特徴量生成方法

参考文献

• [BTF] [2203.05550] Back to the Feature: Classical 3D Features are (Almost) All You Need for 3D Anomaly Detection

• [ImageNet] ImageNet: A large-scale hierarchical image database | IEEE Conference Publication | IEEE Xplore

• [HOG] Histograms of oriented gradients for human detection | IEEE Conference Publication | IEEE Xplore

• [SIFT] Distinctive Image Features from Scale-Invariant Keypoints | SpringerLink

• [FPFH] Fast Point Feature Histograms (FPFH) for 3D registration | IEEE Conference Publication | IEEE Xplore