ビジネスを取り巻くAI・DXの現状と未来～第4回  データ分析の進め方（データサイエンティストの視点）

感覚とは違うデータの捉え方

株式会社ブレインパッド・山崎 清仁（以下、山崎）シリーズでお届けしている『ビジネスを取り巻くAI・DXの現状と未来』の4回目となります。角谷さん、よろしくお願いします。 

株式会社ブレインパッド・角谷 督（以下、角谷） 今回は、ビジネスシーンでのデータの見方や考え方、そして時々見受けられるデータサイエンティストが陥りがちな勘違いについて取り上げたいと思います。

年初から新NISAの新たな投資枠で株式投資を考えている方も多いと思います。ネットの書き込みや動画サイトなどでも、データに関する間違った理解から勘違いが散見されているので、まずは一般的なこの話題から始めたいと思います。

山崎　宜しくお願いします。

角谷　ドルコスト平均法^※1による貯蓄の有効性がマネー雑誌やYouTubeなどの媒体で喧伝されています。ドルコスト平均法によって、時間分散することは高値掴みをしないという点で有効なことは間違いないと思います。

しかし、投資開始時点で一括に投資する場合と比べると、市場リスクに対するエクスポージャー（リスクに暴露している金額）が少ない分、機会損失が発生することとなります。期待リターンに対する見通しが投資時期によって変わらないのであれば、早く投資したほうが合理的です。多くの余剰資金がある場合には、わざわざ少しずつ買い足していく理由はないと考えます。

※1「ドルコスト平均法」は金融商品における投資手法の一つで、日々価格変動する金融商品を一度に購入するのではなく、一定金額で定期的に積み立て投資する方法です。

山崎　投資に関しての考え方は様々あると思いますが、データの捉え方としては一般に言われている手法を鵜呑みにするのではなく、状況も合わせて見なければならないということですね。

角谷　投資関連でもうひとつ。「100円投資して50％下落すると50円になってしまい、それが100円に戻るには100％上昇しないといけないので、下落すると価格が戻るのが大変だ」という話を耳にすることがあります。 でも標準化された（期待値をゼロとした）株価収益率が上下で対称と考えると変な話ですよね。逆に50円が100円になり、その後50円に戻ったとしたら、「100％上昇して100円になったのに、50％しか下落しなくても元の50円に戻ってしまう」ということになりますから、上記で計算される収益率が正規分布に従い、対称な分布であるなら投資によって儲かるとは思えません。

これもデータ（数値）の見方としては誤りで、連続収益率で考えるとリターンは対数階差^※2で考えるべきです。このとき、下落率は log50-log100 、上昇率は log100-log50 となり、正負で対称となります。このように株価が指数的に変化すると考えると、伸び率は対数階差で表す方が適切です。このようなケースは、感覚でデータを見ると勘違いしてしまう典型例だと思います。

※2 階差とは前期と当期の数値の差額であり、対数階差は対数変換された値の階差をとったものです。

山崎　投資のケースで例示いただきましたが、実際の我々が直面するデータ分析の現場では、どのような間違いが起こりやすいですか。

角谷　まず、一般的なデータ分析の進め方ですが次の順番で進めることが多いと思います。

1. 現状把握
2. 課題の設定
3. 分析設計
4. 分析の実施
5. 分析結果の解釈とまとめ

「１．現状把握」においては、因果関係と単なる相関関係を間違えて捉えてはいけませんし、直感によってデータの見方にバイアスが掛かる場合も考えられます。

「２．課題の設定」では、解決可能な課題である必要がありますし、それがなぜ課題なのかを考える必要があります。課題を解くことで具体的な意思決定や行動に繋がるように、何がわかる（解決される）と意思決定できるのかを考えて課題を設定するということです。分析するまでもなく、ロジカルに考えれば意思決定できるような課題（前述の例で言えば、一括投資すべきか、積み立て投資がよいのか等）が設定されていることもありますから。

山崎　我々が得意とするデータ分析の業務であっても、そもそも分析に入ってよいか、という「１．現状把握」「２．課題の設定」を省いてはならないということですね。

角谷　はい。課題設定が明確にできれば次のステップに進めます。

「３．分析設計」では、必要なデータの期間や種類を調べ、欠損状況を含め、十分なデータが集まるかどうかを検討する必要があります。そして「４．分析の実施」では、分析結果のまとめや解釈性にも影響を与えることを考えれば、なるべくわかりやすい手法で実施するのが望ましいでしょう。

分析における重要な観点は、主に「主観的なバイアスが生じるリスク」、「データから因果関係や規則性を正しく見極める」、「明確な目的意識を持つ」ということになります。

山崎　分析における重要な観点を挙げていただきましたが、より詳細に教えていただけますでしょうか。

角谷　それでは、実際にデータから因果関係を見誤る例として、「交絡因子の存在」、「取得データが打ち切りデータである」ケースを簡単な例で紹介したいと思います。また、人の直感が当てにならないことも、数値例でお示しします。

プロジェクトに見るデータ分析の留意点（1） 交絡因子

山崎　では、ひとつめの交絡因子から詳細をご説明していただきたいです。

角谷　有名な例では、シンプソンのパラドックスがあります。以下に簡単な例を示します。

シンプソンのパラドックスの例

疾病Xの発症に対して、危険因子Aと危険因子Bのリスクを比較するため、危険因子Aと危険因子Bをそれぞれ単独に保有する4,000人の被験者の母集団を調べた。この集団の男女構成は以下の表であったとする。

　

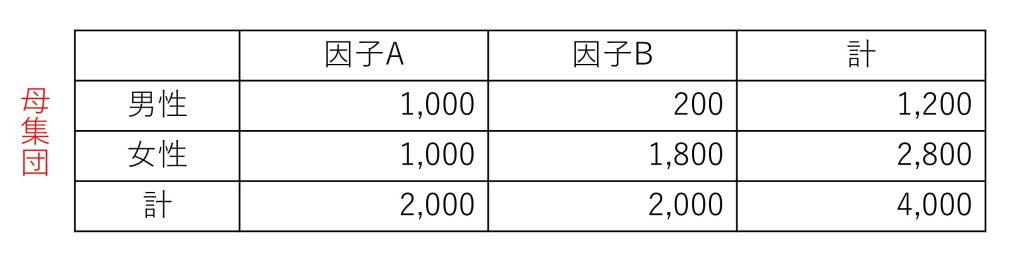
これらの集団の疾病Xの発症件数、発症比率を下記の表の通りとすると、母集団全体では、因子Bによる発症リスクが因子Aよりも高いが、男女別にみると、女性に対しては因子Aのリスクが因子Bよりも高い。

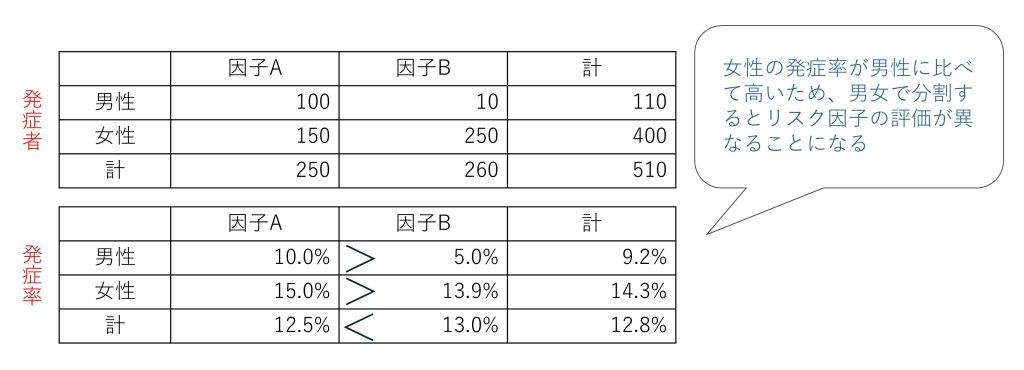
角谷　この例のように、性別をファクターとして捉えるかどうかによって因子の影響が変わってしまいます。

山崎　危険因子と性別の間に交互作用がある可能性があるということですね。もし交互作用がある因子（上記では性別）がわからない場合は、どのように見るのがよいのでしょうか。

角谷　上記では、因子Bの観察データは大きく女性に偏っていますし、母集団も女性の方が多いです。そのデータから、因子Aと因子Bでは全体で因子Bの方がリスクが大きいと判断されたのですが、もし男女比が同じであれば、全体としても因子Aのリスクの方が大きくなるはずです。つまり、男女比率が偏った集団間で検証すると、このような交絡バイアス（性別で効果の差がある）が生じてしまいます。全体としての効果を分析するためには、男女比をなるべく一致させたデータを扱う必要があります。

もし、性別が交絡因子であるとわかっていない場合でも、無作為割付や層別サンプリング（いくつかの部分集団（層）に分けて各層から無作為抽出する）によって偏りを無くすことができますが、層別サンプリングは、交絡因子候補が多いと各層のサンプルが少なくなってしまうのが難点です。

例え、予め交絡因子がわかっていて交互作用が無い場合でも、対象データを限定してバイアスが発生しないようにする場合があります。例えば、肺ガンに対して、ある薬がガンの発生を抑制するかどうかを調べる場合では、喫煙が肺ガンの主因子であるとわかっているなら、非喫煙者に対象を絞って検証することで、バイアスを無くすことができます。

他にも、交絡因子のレベルをマッチングさせる方法があり、実証分析する際には、うまくデザインする必要があります。

山崎　交絡因子とは、主要因ではない因子が主な因子と相関が強いため、因果関係と関連づけてしまう可能性のある因子をいいますが、交絡因子か主因子かの判別は難易度が高いですね。

単純に統計的にデータだけを見るだけでなく、その因果関係をはかるために主題に対する知識が必要になり、実ビジネスでは重要だということが分かりました。

プロジェクトに見るデータ分析の留意点（2） 打ち切りデータ

角谷　次に、このようなバイアスに関して理解していても、取得データに偏りがあることに気づかないことがあります。例えば、筆記試験と面接試験を実施して、それぞれに点数をつけて合計点で合格者を決める場合などです。この２つの試験の点数の間には、相関がないとします。以下の図１のような状態です。

２つの試験の結果には相関がないため、データは丸く散らばっています。そして、合格者は青い線より右側の人だけになります。この合格者だけをサンプリングしたら、どうなるでしょうか。図２をご覧ください。筆記試験が高い受験者は面接試験が低いという結果になってしまいます。

山崎　つまり、合格のための点数で打ち切った集団である合格者は、筆記試験の点数と面接試験の点数に相関をもった属性となってしまうという例ですね。

角谷　これは非常にわかりやすいケースですが、ビジネスにおいても類似した事象が生じていないとも限りません。例えば、金融機関の与信審査では何らかの審査基準で諾否を決定していると思いますが、与信を実行した後に得られるデータは審査で承認された信用度の高いデータとなっています。よって、データ分析においては、与信を申し込んだ全体のデータとは傾向が異なる可能性があることに注意を払う必要があるでしょう。

山崎　事前にスクリーニングされているデータを扱う場合などでは気をつけるべきですね。

プロジェクトに見るデータ分析の留意点（3） 直感的な理解による誤り

山崎　データ分析の現場では、因果関係がなければ相関は無いのはその通りですが、相関があるから因果関係があるわけではない、という話は他にもよく聞きますよね。

角谷　はい。因果関係についての洞察は、マーケティング分析でも重要ですね。当たり前ですが、店頭に陳列しているものしか売れないので、売れているからといって必ずしも人気があるとも限らないということはよく言われます。

あるコンビニ店舗で、売上を上げるため、売れない商品を陳列から除いてしまうという判断をしたとします。もし、人々がコンビニ店に行く理由が、お店に行けば大抵の日用品が揃っているからという理由だったとすると、来店者数が減ってしまうという現象が起きるでしょう。

山崎　極端な例かもしれませんが、品揃えを少なくしてしまった結果、来店者が減り、売上が減るということですね。

角谷　つまり、データは結果を表しているだけで、売れている原因の本質を探る姿勢が重要です。数理的な訓練を受けているデータサイエンティストですら、主観から逃れて客観的に判断することは難しいです。我々も普段からバイアスを持ちやすい存在だと認識していることが重要です。

山崎　別の角度から直感による誤りとなるような例をもうひとつ挙げて頂けますでしょうか。

角谷　ある商品の品質を判別するために、誤差１％（正例を負例と間違える確率が１％、負例を正例と間違える確率も１％）である判別機を作成出来たとします。もちろん、この判別機は非常に高い精度といえます。例えば、ここにコピー機が十万台あるとして、そのうちの1台が不良品だったとします。このとき、ランダムに1台を選び出し、判別機が“不良品”と判断したとします。この結果を信じて行動してもよいでしょうか。

山崎　精度が高い判別機なので、信用したくなります。不良品の割合がわからない中で判別機だけを信用すれば、故障率が高い（不良品が多い）のではないかと心配になります。

角谷　それでは、判別機が不良品と判別した時に、実際に不良品である確率を求めましょう。判定結果をYとし、正解をY*とします。そうすると、次の式を計算すればよいことになります。

　　$$P(Y*=不良品｜Y=不良品)＝P(Y*＝不良品、Y=不良品）／P(Y＝不良品） （１）$$

山崎　記号が分かりづらいので補足説明をお願いします。 

角谷　左辺「P(Y*=不良品｜Y=不良品)」は題意のとおり「判別機が不良品と判断したときの正解である確率」です。

そして、右辺の分子「P(Y*＝不良品、Y=不良品）」は同時確率を表します。「不良品の確率」と「不良品を正確に不良品であると見分けることが出来る確率」の掛け算となります。右辺の分母「P(Y＝不良品）」は「判別機が不良品と判断する確率（正当は問わない）」です。

この確率を正しく計算すると、

　　$$P(Y*＝不良品、Y=不良品）＝1/10万×99\%＝99/1000万　　　　　　　（２）$$

　　$$P(Y＝不良品）＝P(Y*＝不良品、Y=不良品）＋P(Y*＝良品、Y=不良品）$$

　　$$　　　　　　　＝（２）式の値　＋ P(Y*＝良品、Y=不良品）　　　　（３）$$

となります。ここで、P(Y*＝良品、Y=不良品）は「良品の確率」と「良品を不良品と判断してしまう確率の同時確率なので、99999/10万×1\%=99999/1000万　です。

すなわち、

　　$$P(Y＝不良品)＝99/1000万+99999/1000=100098/1000万　（４）$$

となり、式（２）と式（４）から式（１）が計算でき、

　　$$P(Y*=不良品｜Y=不良品）＝（２）/（４）≒0.1\%$$

となります。いかがでしょうか。

山崎　確かに直感が裏切られた感覚です。

角谷　そう思われると思いますが、このように故障確率が非常に小さい場合では、精度が高い判別機も役に立たないことがわかります。かなり有名な例ですが、最後にもうひとつ、モンティホール問題をみてみましょう。

山崎　それは私も知っています。次のような問題ですね。

 モンティホール問題

いま、挑戦者と司会者が居て、そこには３つの扉があるとする。そのうち、1つだけの扉が正解で、それを開けると商品の高級車が置いてあり、残りは不正解であり高級車はない。どれが正解かは不明であり、挑戦者は1つだけ扉を選ぶことができる。そして、挑戦者が1つの扉を選んだあとは、残りは扉2つである。

司会者は、この残り２つの扉の中から、不正解のものを選び、その扉を開けて不正解であることを挑戦者に知らせ、挑戦者に対して、「選び直してもいいですよ。」と言う。ここで、挑戦者は選び直すべきか、最初に選んだ扉のままにしたほうがよいか。

という問題ですね。 

角谷　よくある間違いが、「全ての扉の正答率は1/3であり、1つだけ外れが取り除かれたから、残りの正答率はどちらも1/2であり、選び直しても、選び直さなくても同じである」というのが直感的な回答です。

山崎　しかし「選び直す」が良いんですね。

角谷　正解です。最初に選んだ扉の正答率は1/3で、必ず残りの2つの扉には外れがあり、それを開けるだけなので、最初の選択の正答率は変わらず1/3のままです。

一方、選択されなかった２つの扉に当たりが入っている確率は2/3です。扉は２つありますが、２つの扉の中から司会者が外れを教えてくれたので、残りの1つの扉の当たる確率は2/3に増大します。つまり、最初に選択された扉は情報が増大していないが、選択されなかった残りの扉は情報が増大しており、選び直すほうが確率は高くなります。

山崎　知っていれば間違わないと思いますが、なぜ多くの人は間違うのでしょうか。

角谷　もう少し分かりやすく問題を考えてみましょう。1000個の扉があり、そのうち一つが正解で、999個の扉が不正解という前提に置き直してみます。先ほどと同じように挑戦者が一つの扉を選び、司会者が残りの999個のうち999個の外れの扉を教えてくれるとしたら、ほとんどの人は、”選び直すほうがよい”と答えるのではないでしょうか。実は、この状況は元の３つの扉の問題と同じ考え方なんです。

つまり、1/2や1/3といった大きく異ならない確率を議論する場合は、人の直観はかなりいい加減な判断をもたらすといえるのではないでしょうか。

山崎　直感的な理解による誤りの例として２つの例をみてきましたが、直感で間違ってしまうことを避ける方法はありますか？

角谷　そうですね。 例えば、

1. 簡単でわかりやすい数値や極端な数値に置き換えて考えてみる
2. 直観に頼らない多くの分析経験を積む
3. 他人の経験から学ぶ

といったことでも思い込みや直感による誤りは避けることが出来ると思います。

山崎　今回は、プロジェクトに見るデータ分析の留意点という話題でお話しさせて頂きました。ありがとうございました。